题目内容
如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE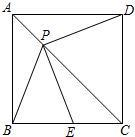 =PB.
=PB.(1)求证:①PE=PD;②PE⊥PD;
(2)设AP=x,△PBE的面积为y.
①求出y关于x的函数关系式,并写出x的取值范围;
②当x取何值时,y取得最大值,并求出这个最大值.
分析:(1)可通过构建全等三角形来求解.过点P作GF∥AB,分别交AD、BC于G、F,那么可通过证三角形GPD和EFP全等来求PD=PE以及PE⊥PD.在直角三角形AGP中,由于∠CAD=45°,因此三角形AGP是等腰直角三角形,那么AG=PG,而PB=PE,PF⊥BE,那么根据等腰三角形三线合一的特点可得出BF=FE=AG=PG,同理可得出两三角形的另一组对应边DG,PF相等,因此可得出两直角三角形全等.可得出PD=PE,∠GDP=∠EPF,而∠GDP+∠GPD=90°,那么可得出∠GPD+∠EPF=90°,由此可得出PD⊥PE.
(2)求三角形PBE的面积,就要知道底边BE和高PF的长,(1)中已得出BF=FE=AG,那么可用AP在等腰直角三角形AGP中求出AG,GP即BF,FE的长,那么就知道了底边BE的长,而高PF=CD-GP,也就可求出PF的长,可根据三角形的面积公式得出x,y的函数关系式.然后可根据函数的性质及自变量的取值范围求出y的最大值以及对应的x的取值.
(2)求三角形PBE的面积,就要知道底边BE和高PF的长,(1)中已得出BF=FE=AG,那么可用AP在等腰直角三角形AGP中求出AG,GP即BF,FE的长,那么就知道了底边BE的长,而高PF=CD-GP,也就可求出PF的长,可根据三角形的面积公式得出x,y的函数关系式.然后可根据函数的性质及自变量的取值范围求出y的最大值以及对应的x的取值.
解答:(1)证明:①过点P作GF∥AB,分别交AD、BC于G、F.如图所示.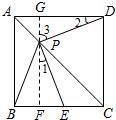
∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,
△AGP和△PFC都是等腰直角三角形.
∴GD=FC=FP,GP=AG=BF,∠PGD=∠PFE=90度.
又∵PB=PE,
∴BF=FE,
∴GP=FE,
∴△EFP≌△PGD(SAS).
∴PE=PD.
②∴∠1=∠2.
∴∠1+∠3=∠2+∠3=90度.
∴∠DPE=90度.
∴PE⊥PD.
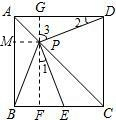
(2)解:①过P作PM⊥AB,可得△AMP为等腰直角三角形,
四边形PMBF为矩形,可得PM=BF,
∵AP=x,∴PM=
x,
∴BF=PM=
x,PF=1-
x.
∴S△PBE=
BE×PF=BF•PF=
x•(1-
x)=-
x2+
x.
即y=-
x2+
x.(0<x<
).
②y=-
x2+
x=-
(x-
)2+
∵a=-
<0,
∴当x=
时,y最大值=
.

∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,
△AGP和△PFC都是等腰直角三角形.
∴GD=FC=FP,GP=AG=BF,∠PGD=∠PFE=90度.
又∵PB=PE,
∴BF=FE,
∴GP=FE,
∴△EFP≌△PGD(SAS).
∴PE=PD.
②∴∠1=∠2.
∴∠1+∠3=∠2+∠3=90度.
∴∠DPE=90度.
∴PE⊥PD.
(2)解:①过P作PM⊥AB,可得△AMP为等腰直角三角形,
四边形PMBF为矩形,可得PM=BF,
∵AP=x,∴PM=
| ||
| 2 |

∴BF=PM=
| ||
| 2 |
| ||
| 2 |
∴S△PBE=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
即y=-
| 1 |
| 2 |
| ||
| 2 |
| 2 |
②y=-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
∵a=-
| 1 |
| 2 |
∴当x=
| ||
| 2 |
| 1 |
| 4 |
点评:本题主要考查了正方形,矩形的性质,全等三角形的判定以及二次函数的综合应用等知识点,通过构建全等三角形来得出相关的边和角相等是解题的关键.

练习册系列答案
相关题目
 14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )
14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )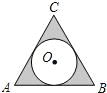 如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为
如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为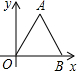 如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A
如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A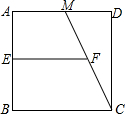 如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF=
如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF= 如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )
如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )