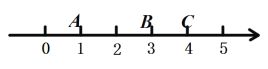ЬтФПФкШн
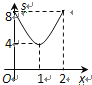
ЁОЬтФПЁПЮЊСЫЁАТЬЛЏЛЗОГЃЌУРЛЏМвдАЁБЃЌ3дТ12ШеЃЈжВЪїНкЃЉЩЯЮч8ЕуЃЌФГаЃ901ЁЂ902АрЭЌбЇЭЌЪБВЮМгвхЮёжВЪїЃЎ901АрЭЌбЇЪМжевдЭЌвЛЫйЖШжжжВЪїУчЃЌжжжВЪїУчЕФПУЪ§y1гыжжжВЪБМфx(аЁЪБ)ЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЛ902АрЭЌбЇПЊЪМвд1аЁЪБжжжВ40ПУЕФЫйЖШЙЄзїСЫ1.5аЁЪБКѓЃЌвђашИќЛЛЙЄОпЖјЭЃЯТанЯЂАыаЁЪБЃЌИќЛЛЙЄОпКѓжжжВЫйЖШЬсИпжСдРДЕФ1.5БЖ.
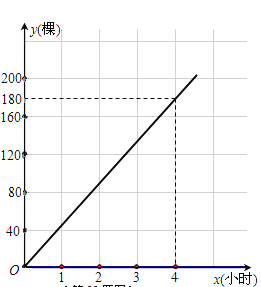
ЃЈ1ЃЉЧѓ902АрЭЌбЇЩЯЮч11ЕуЪБжжжВЕФЪїУчПУЪ§ЃЛ
ЃЈ2ЃЉЗжБ№ЧѓГі901АржжжВЪ§СПy1ЁЂ902АржжжВЪ§СПy2гыжжжВЪБМфxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂдкЫљИјзјБъЯЕЩЯЛГіy2ЙигкxЕФКЏЪ§ЭМЯѓЃЛ
ЃЈ3ЃЉвбжЊЙКТђЪїУчВЛЖргк120ПУЪБЃЌУППУЪїУчЕФМлИёЪЧ20дЊЃЛЙКТђЪїУчГЌЙ§120ПУЪБЃЌГЌЙ§ЕФВПЗжУППУМлИё17дЊ.ШєБОДЮжВЪїЫљЙКЪїУчЕФЦНОљГЩБОЪЧ18дЊЃЌдђСНАрЭЌбЇЩЯЮчМИЕуПЩвдЙВЭЌЭъГЩБОДЮжВЪїШЮЮёЃП
ЁОД№АИЁПЃЈ1ЃЉ120ПУЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉСНАрЭЌбЇЩЯЮч12ЕуПЩвдЙВЭЌЭъГЩБОДЮжВЪїШЮЮё.
ЁОНтЮіЁПЗжЮіЃК![]() жБНгНјааМЦЫуМДПЩ.
жБНгНјааМЦЫуМДПЩ.
![]() гУД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§НтЮіЪНМДПЩ, 902АрЕФвЊЗжГЩ3ЖЮ.
гУД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§НтЮіЪНМДПЩ, 902АрЕФвЊЗжГЩ3ЖЮ.
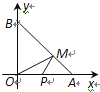
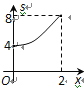
![]() ЕБx=2ЪБЃЌСНАрЭЌбЇЙВжВЪї150ПУЃЌ
ЕБx=2ЪБЃЌСНАрЭЌбЇЙВжВЪї150ПУЃЌ![]() ЦНОљГЩБОЃКВЛЗћКЯЬтвтЃЛЃЌx>2ЃЌСНАрЙВжВЪїЃЈ105x-60ЃЉПУ.СаГіЗНГЬ
ЦНОљГЩБОЃКВЛЗћКЯЬтвтЃЛЃЌx>2ЃЌСНАрЙВжВЪїЃЈ105x-60ЃЉПУ.СаГіЗНГЬ![]() ЧѓНтМДПЩ.
ЧѓНтМДПЩ.
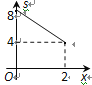
ЯъНтЃКЃЈ1ЃЉ902АрЭЌбЇЩЯЮч11ЕуЪБжжжВЕФЪїУчПУЪ§ЮЊЃК
![]() ЃЈПУЃЉ
ЃЈПУЃЉ
ЃЈ2ЃЉгЩЭМПЩжЊЃЌy1ЪЧЙигкxЕФе§БШР§КЏЪ§ЃЌПЩЩшy1=k1xЃЌОЙ§ЃЈ4ЃЌ180ЃЉЃЌ
ДњШыПЩЕУ![]()
Ёр![]() ЃЈxЁн0ЃЉ,
ЃЈxЁн0ЃЉ,
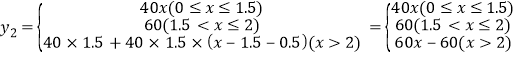 ,
,
y2ЙигкxЕФКЏЪ§ЭМЯѓШчЭМЫљЪО.
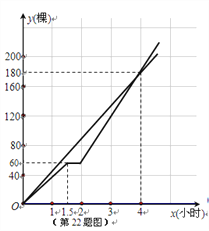
ЃЈ3ЃЉЕБx=2ЪБЃЌСНАрЭЌбЇЙВжВЪї150ПУЃЌ
![]() ЦНОљГЩБОЃК
ЦНОљГЩБОЃК
ЫљвдЃЌx>2ЃЌСНАрЙВжВЪїЃЈ105x-60ЃЉПУ.
![]() гЩЬтвтПЩЕУЃК
гЩЬтвтПЩЕУЃК
НтЕУЃКx=4.
![]() ,
,
ЫљвдЃЌСНАрЭЌбЇЩЯЮч12ЕуПЩвдЙВЭЌЭъГЩБОДЮжВЪїШЮЮё.
ЕуОІЃКПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§НтЮіЪНЃЌвЛдЊвЛДЮЗНГЬЕФгІгУЃЌзЂвтЗжРрЬжТл
ЕФЪ§бЇЫМЯыЗНЗЈ.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
23
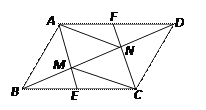
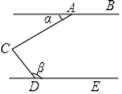
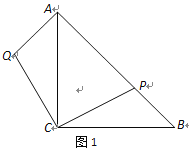
ЁОЬтФПЁПдкЕШбќжБНЧЁїABCжаЃЌЃЌAC=BCЃЌЕуPдкаББпABЩЯЃЈAP>BPЃЉ.зїAQЁЭABЃЌЧвAQ=BPЃЌСЌНсCQЃЈШчЭМ1ЃЉ.
ЃЈ1ЃЉЧѓжЄЃКЁїACQЁеЁїBCPЃЛ
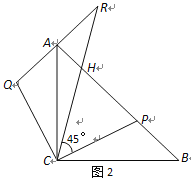
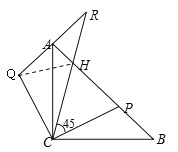
ЃЈ2ЃЉбгГЄQAжСЕуRЃЌЪЙЕУЁЯRCP=45ЁуЃЌRCгыABНЛгкЕуHЃЌШчЭМ2.
ЂйЧѓжЄЃКCQ2=QAЁЄQR ЃЛ
ЂкХаЖЯШ§ЬѕЯпЖЮAHЁЂHPЁЂPBЕФГЄЖШТњзуЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩ.
ЁОД№АИЁПМћНтЮі
ЁОНтЮіЁПЗжЮіЃК![]() жЄУї
жЄУї![]() ИљОн
ИљОн![]() МДПЩжЄУїЁїACQЁеЁїBCP.
МДПЩжЄУїЁїACQЁеЁїBCP.
![]() ЂйИљОнСНзщНЧЖдгІЯрЕШЕФСНИіШ§НЧаЮЯрЫЦжЄУїІЄCQRЁзІЄAQCЃЌИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЕУЕН
ЂйИљОнСНзщНЧЖдгІЯрЕШЕФСНИіШ§НЧаЮЯрЫЦжЄУїІЄCQRЁзІЄAQCЃЌИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЕУЕН![]() МДПЩжЄУї.
МДПЩжЄУї.
ЂкСЌНгQHЃЌжЄУїЁїQCHЁеЁїPCHЃЌЕУЕНHQ=HP. дк![]() жаЃЌгУЙДЙЩЖЈРэМДПЩЕУЕНAHЁЂHPЁЂPBЕФЪ§СПЙиЯЕ.
жаЃЌгУЙДЙЩЖЈРэМДПЩЕУЕНAHЁЂHPЁЂPBЕФЪ§СПЙиЯЕ.
ЯъНтЃКЃЈ1ЃЉЁп![]()
Ёр![]()
гжЁпAQЁЭAB,
Ёр![]()
дкІЄACQКЭІЄBCPжа
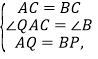
ЁрЁЁЁїACQЁеЁїBCP (SAS)
ЃЈ2ЃЉЂйгЩЃЈ1ЃЉжЊЁїACQЁеЁїBCPЃЌдђ![]()
Ёп![]() ЁЯRCP=45ЁуЃЌ
ЁЯRCP=45ЁуЃЌ
ЁрЁЯACR+ЁЯPCB=45Ёу,
ЁЁЁрЁЯACR+ЁЯQCA =45ЁуЃЌ
МДЁЯQCR =45Ёу=ЁЯQAC ,
ЁЁгжЁЯQЮЊЙЋЙВНЧЃЌ
ЁрІЄCQRЁзІЄAQCЃЌ
![]()
ЁрCQ2=QAЁЄQR.
Ђк![]() .
.
РэгЩЃКСЌНгQHЃЌгЩЃЈ1ЃЉЃЈ2ЃЉЬтжЊЃК![]() ЃЌCQ=CP.
ЃЌCQ=CP.
гжCH ЪЧЁїQCHКЭЁїPCHЕФЙЋЙВБпЃЌ
ЁрЁїQCHЁеЁїPCHЃЈSASЃЉ.
ЁрHQ=HP.
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
гжгЩЃЈ1ЃЉжЊЃКQA=PBЃЌ
Ёр![]() .
.

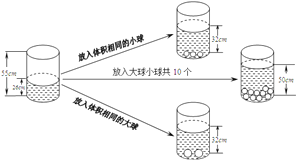
ЁОЬтФПЁПИіЬхЛЇаЁЭѕдкЩЯжмШевдУПЧЇПЫ4дЊТђНјН№З№ЩНЯЪЫё![]() ЃЌНјШыХЉУГЪаГЁКѓЙВеМ5ИіЬЏЮЛЃЌУПИіЬЏЮЛзюЖрШнФЩ
ЃЌНјШыХЉУГЪаГЁКѓЙВеМ5ИіЬЏЮЛЃЌУПИіЬЏЮЛзюЖрШнФЩ![]() ЯЪЫёЃЌУПИіЬЏЮЛЕФЪаГЁЙмРэМлЮЊУПЬь20дЊЃЌЯТБэЮЊБОжмФкЯЪЫёУПЬьЕФЯњЪлМлИёгыЧАвЛЬьЯрБШМлИёЕФеЧЕјЧщПіЃЈеЧМЧЮЊе§ЃЌЕјМЧЮЊИКЃЉ.аЧЦквЛЕФМлИёЪЧдкжмШеУПЧЇПЫ4дЊТђНјМлИёЛљДЁЩЯеЧСЫ1.3дЊ.
ЯЪЫёЃЌУПИіЬЏЮЛЕФЪаГЁЙмРэМлЮЊУПЬь20дЊЃЌЯТБэЮЊБОжмФкЯЪЫёУПЬьЕФЯњЪлМлИёгыЧАвЛЬьЯрБШМлИёЕФеЧЕјЧщПіЃЈеЧМЧЮЊе§ЃЌЕјМЧЮЊИКЃЉ.аЧЦквЛЕФМлИёЪЧдкжмШеУПЧЇПЫ4дЊТђНјМлИёЛљДЁЩЯеЧСЫ1.3дЊ.
аЧЦк | вЛ | Жў | Ш§ | ЫФ | Юх |
гыЧАвЛЬьЯрБШМлИёЕФеЧЕјЧщПі/дЊ | +1.3 | Ѓ0.1 | +0.25 | +0.2 | Ѓ0.5 |
ЕБЬьЕФНЛвзСП/ | 2500 | 2000 | 3000 | 1500 | 1000 |
ЃЈ1ЃЉЯЪЫёЯњЪлзюИпМлИёЮЊУПЧЇПЫЖрЩйдЊЃП
ЃЈ2ЃЉаЁЭѕдкЩЯжмШевдУПЧЇПЫ4дЊТђНјН№З№ЩННтЫё![]() ЃЌНјШыХњЗЂЪаГЁКѓЙВеМ5ИіЬЏЮЛЃЌаЁЭѕдкЯњЪлЙ§ГЬжаВЩгУж№ВНМѕЩйЬЏЮЛИіЪ§ЕФЗНЗЈРДНЕЕЭГЩБОЃЌдіМгЪевцЃЌетбљЫћдкБОжмЕФТђТєжаЙВзЌСЫЖрЩйЧЎЃПЧыФуАяЫћЫувЛЫуЃП
ЃЌНјШыХњЗЂЪаГЁКѓЙВеМ5ИіЬЏЮЛЃЌаЁЭѕдкЯњЪлЙ§ГЬжаВЩгУж№ВНМѕЩйЬЏЮЛИіЪ§ЕФЗНЗЈРДНЕЕЭГЩБОЃЌдіМгЪевцЃЌетбљЫћдкБОжмЕФТђТєжаЙВзЌСЫЖрЩйЧЎЃПЧыФуАяЫћЫувЛЫуЃП