Question

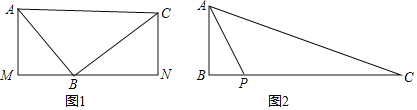
【题目】某高速铁路位于某省南部，是国家“八纵八横”高速铁路网的重要连接通道，也是某省“三横五纵”高速铁路网的重要组成部分．东起日照，向西贯穿临沂、曲阜、济宁、菏泽，与郑徐客运专线兰考南站接轨．工程有一段在一条河边，且刚好为东西走向．B处是一个高铁维护站，如图①，现在想过B处在河上修一座桥，需要知道河宽，一测量员在河对岸的A处测得B在它的东北方向，测量员从A点开始沿岸边向正东方向前进300米到达点C处，测得B在C的北偏西30度方向上．

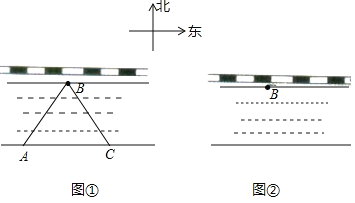
（1）求所测之处河的宽度；（结果保留的十分位）

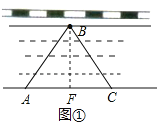
（2）除（1）的测量方案外，请你再设计一种测量河宽的方案，并在图②中画出图形．

Answer 1

【答案】（1）所测之处江的宽度为190.5m；（2）见解析.

【解析】

解：（1）过点B作BF⊥AC于F，根据题意得到∠EAB＝45°，∠GCB＝30°，AC＝300m，求得∠FBA＝45°，∠CBF＝30°，得到BF＝AF，解直角三角形即可得到结论；

（2）构造相似三角形，根据相似三角形的性质得到方程即可得到结论．．

（1）过点B作BF⊥AC于F，

由题意得：∠EAB＝45°，∠GCB＝30°，AC＝300m，

∴∠FBA＝45°，∠CBF＝30°，

∴BF＝AF，

∴FC＝300﹣AF＝300﹣BF（m），

在Rt△BFC中，tan∠CBF＝，

∴tan30°＝，

∴，

解得：BF﹣150（3﹣）≈190.5（m），

答：所测之处江的宽度为190.5m；

（2）①在河岸取点A，使B垂直于河岸，延长BA至C，测得AC做记录，

②从C沿平行于河岸的方向走到D，测得CD，做记录，

③B0与河岸交于E，测AE，做记录．根据△BAE～△BCD，

得到比例线段，从而求出河宽AB．