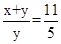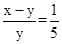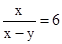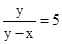题目内容
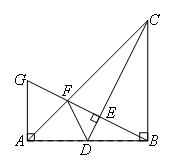
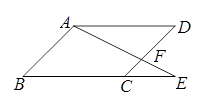
如图,□ABCD中,E为BC延长线上一点,AE交CD于点F,若 ,AD=2,∠B=45°,
,AD=2,∠B=45°, ,求CF的长.
,求CF的长.
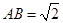 ,AD=2,∠B=45°,
,AD=2,∠B=45°,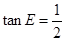 ,求CF的长.
,求CF的长.
 .
.试题分析:过点A作AM⊥BE于点M.首先利用已知条件求出BE=BM+ME=3,再利用平行四边形的性质求出CE=BE-BC=1,最后通过证明△ADF∽△ECF,有相似三角形的性质即可求出CF的长.
试题解析:过点A作AM⊥BE于点M.
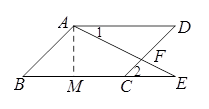
在Rt△ABM中,
∵∠B=45°,
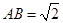 ,
,∴
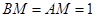 .∵
.∵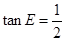 ,
,∴
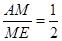 .
. ∴EM=2.
∴BE=BM+ME=3.
∵四边形ABCD是平行四边形,
∴BC=AD=2,DC=AB=
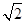 ,AD∥BC.
,AD∥BC.∴CE=BE-BC=1.
∵AD∥BC,
∴∠1=∠E,∠D=∠2.
∴
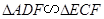 .
.∴
 .
.∵DC=
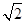 ,
,∴
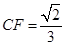 .
.考点: 1.相似三角形的判定与性质;2.平行四边形的性质;3.解直角三角形.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
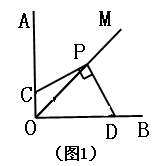
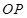 的长.(提示:请先在备用图中画出相应的图形,再求
的长.(提示:请先在备用图中画出相应的图形,再求
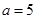 ,
,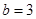 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________. ,
,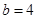 时,
时,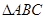 为圆O的内接三角形,
为圆O的内接三角形,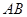 为直径,过C作
为直径,过C作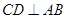 于D,设
于D,设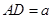 ,BD=b.
,BD=b.
 表示线段OC,CD;
表示线段OC,CD;
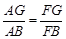 ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=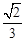 AB;④S△ABC ="5" S△BDF,其中正确的结论序号是_____________.
AB;④S△ABC ="5" S△BDF,其中正确的结论序号是_____________.