Question

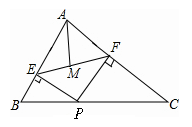
如图，在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为（　　）

A．2

B．2.4

C．2.6

D．3

Answer 1

B．

试题分析：先求证四边形AFPE是矩形，再根据直线外一点到直线上任一点的距离，垂线段最短，利用三角形面积公式即可求得AP最短时的长，然后即可求出AM最短时的长：
在△ABC中，AB=6，AC=8，BC=10，∴∠BAC=90°.
∵PE⊥AB，PF⊥AC，∴四边形AFPE是矩形.∴EF=AP．
∵M是EF的中点，∴AM=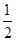AP.
根据直线外一点到直线上任一点的距离，垂线段最短，即AP⊥BC时，AP最短，同样AM也最短，
∴当AP⊥BC时，由三角形面积公式得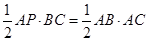，即，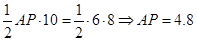
∴AP最短时，AP=4.8∴当AM最短时，AM=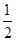AP=2.4．
故选B．