题目内容
点A(-2,0)是x轴上一点,将线段OA绕着点O逆时针方向旋转90°后,再伸长为原来的2倍得到线段OB.(1)求直线AB所对应的一次函数的解析式;
(2)设反比例函数
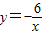 与直线AB相交于C、D两点,求△AOC和△BOD的面积之比.
与直线AB相交于C、D两点,求△AOC和△BOD的面积之比.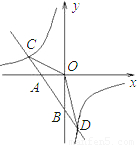
【答案】分析:(1)根据点A(-2,0)是x轴上一点,将线段OA绕着点O逆时针方向旋转90后,再伸长为原来的2倍得到线段OB,可求出点B的坐标,然后即可求出直线AB所对应的一次函数的解析式;
(2)由反比例函数 与直线AB相交于C、D两点,求出C,D两点的坐标,再分别求出△AOC和△BOD的面积即可求出答案.
与直线AB相交于C、D两点,求出C,D两点的坐标,再分别求出△AOC和△BOD的面积即可求出答案.
解答:解:(1)根据点A(-2,0)是x轴上一点,将线段OA绕着点O逆时针方向旋转90°后,再伸长为原来的2倍得到线段OB,
∴点B的坐标是(0,-4),设直线方程为:y=kx+b,把A,B分别代入解得:k=-2,b=-4,
直线AB所对应的一次函数的解析式为:y=-2x-4.
(2)∵反比例函数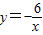 与直线AB相交于C、D两点,
与直线AB相交于C、D两点,
∴ ,解得:
,解得: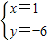 或
或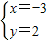 ,
,
∴C(-3,2),D(1,-6),∴S△AOC= ×2×2=2,S△BOD=
×2×2=2,S△BOD= ×4×1=2,
×4×1=2,
∴S△AOC:S△BOD=2:2=1:1,
即△AOC和△BOD的面积之比为:1:1.
点评:本题考查了反比例函数与一次函数的交点及待定系数法求函数解析式,难度较大,主要掌握用待定系数法解函数解析式.
(2)由反比例函数
 与直线AB相交于C、D两点,求出C,D两点的坐标,再分别求出△AOC和△BOD的面积即可求出答案.
与直线AB相交于C、D两点,求出C,D两点的坐标,再分别求出△AOC和△BOD的面积即可求出答案.解答:解:(1)根据点A(-2,0)是x轴上一点,将线段OA绕着点O逆时针方向旋转90°后,再伸长为原来的2倍得到线段OB,
∴点B的坐标是(0,-4),设直线方程为:y=kx+b,把A,B分别代入解得:k=-2,b=-4,
直线AB所对应的一次函数的解析式为:y=-2x-4.
(2)∵反比例函数
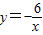 与直线AB相交于C、D两点,
与直线AB相交于C、D两点,∴
 ,解得:
,解得: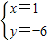 或
或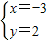 ,
,∴C(-3,2),D(1,-6),∴S△AOC=
 ×2×2=2,S△BOD=
×2×2=2,S△BOD= ×4×1=2,
×4×1=2,∴S△AOC:S△BOD=2:2=1:1,
即△AOC和△BOD的面积之比为:1:1.
点评:本题考查了反比例函数与一次函数的交点及待定系数法求函数解析式,难度较大,主要掌握用待定系数法解函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
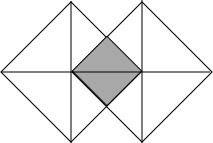 (2013•本溪一模)如图,假设可以随意在图中取点,那么这个点取在阴影部分的概率是( )
(2013•本溪一模)如图,假设可以随意在图中取点,那么这个点取在阴影部分的概率是( ) (2012•朝阳区二模)如图,点P(-3,1)是反比例函数
(2012•朝阳区二模)如图,点P(-3,1)是反比例函数