Question

在一次探究性活动中，教师提出了问题：已知矩形的长和宽分别是2和1，是否存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的2倍？设所求矩形的长和宽分别为x，y
（1）小明从“图形”的角度来研究：所求矩形的周长应满足关系式①________，面积应满足关系式②________，在同一坐标系中画出①②的图象，观察所画的图象，你能得出什么结论？
（2）小丽从“代数”的角度来研究：由题意可列方程组________，解这个方程组，你能得出什么结论？

Answer 1

解：（1）设所求矩形的长和宽分别为x，y，
∵已知矩形的长和宽分别是2和1，新矩形的周长和面积分别是已知矩形周长和面积的2倍，
∴2（x+y）=2×2×（2+1）xy=2×2×1
∴y=-x+6，y=
图象为：

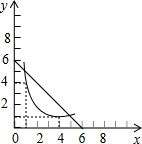
根据图象知：存在两个矩形，能使得新矩形是原矩形的周长与面积的2倍．

（2）将（1）题中得到的两个关系式联立得：

整理得：x²-6x+4=0
∵△=（-6）²-4×4＞0，
∴存在两个矩形，能使得新矩形是原矩形的周长与面积的2倍．
分析：（1）表示出有关周长和面积的两个函数关系式，利用函数的图形判断是否存在这样的矩形即可；
（2）将两个函数关系式联立后得到方程组，利用方程的方法判断是否存在这样的矩形即可．
点评：本题考查了反比例函数的应用，解题的关键是会灵活的运用函数图象交点的意义，以及图象的特点，试题中贯穿了方程思想和数形结合的思想，请注意体会．