题目内容

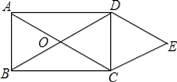
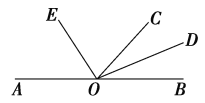
【题目】如图，O是直线AB上一点，OC为任意一条射线，OD平分∠BOC，OE平分∠AOC.

(1)OD与OE的位置关系是______；(2)∠EOC的余角是_______ .

【答案】互相垂直 ∠COD或∠BOD

【解析】

（1）根据平角和角平分线的定义即可求出∠EOD的度数，即可得答案；（2）根据互为余角的和为90°找出即可.

（1）∵OD平分∠BOC，OE平分∠AOC，

∴∠EOC=∠AOC，∠COD=∠COB，

∵∠AOC+∠BOC=180°，

∴∠EOC+∠COD=90°，

∴OD与OE的位置关系是互相垂直.

（2）∵∠COD=∠DOB，∠EOC+∠COD=90°，

∴∠EOC的余角是∠COD或∠DOB，

故答案为：（1）互相垂直；（2）∠COD或∠DOB，

练习册系列答案
相关题目

【题目】如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD．

（1）求证：四边形OCED是菱形．

（2）若AB=6，BC=8，求四边形OCED的周长．

【题目】如图，，点D在边BC上与B、C不重合，四边形ADEF为正方形，过点F作，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：；：：2；；

其中正确的结论的个数是

A. 0 B. 1 C. 2 D. 3

【题目】结合数轴与绝对值的知识回答下列问题：

（1）数轴上表示4和1的两点之间的距离为|4﹣1|=　 　；表示5和﹣2两点之间的距离为|5﹣（﹣2）|=|5+2|=　 　；一般地，数轴上表示数m和数n的两点之间的距离等于|m﹣n|，如果表示数a和﹣2的两点之间的距离是3，那么a=　 　．

（2）若数轴上表示数a的点位于﹣4与2之间，求|a+4|+|a﹣2|的值；

（3）当a=　 　时，|a+5|+|a﹣1|+|a﹣4|的值最小，最小值为　 　．

【题目】观察下列两个等式：2﹣＝2×+1，5﹣＝5×+1，给出定义如下：我们称使等式a﹣b＝ab+1的成立的一对有理数a，b为“共生有理数对”，记为（a，b），如：数对（2，），（5，），都是“共生有理数对”．

（1）数对（﹣2，1），（3，）中是“共生有理数对”的是　 　；

（2）若（m，n）是“共生有理数对”，则（﹣n，﹣m）　 　“共生有理数对”（填“是”或“不是”）；

（3）请再写出一对符合条件的“共生有理数对”为　 　；（注意：不能与题目中已有的“共生有理数对”重复）

（4）若（a，3）是“共生有理数对”，求a的值．

【题目】如图所示： (1)按下列语句画出图形：

①延长AC到D，使CD＝AC；②反向延长CB到E，使CE＝BC；③连接DE.

(2)度量其中的线段和角，你有什么发现？

(3)试判断图中两个三角形的面积是否相等．

【题目】如图，已知抛物线E1：y=x2经过点A（1，m），以原点为顶点的抛物线E2经过点B（2，2），点A、B关于y 轴的对称点分别为点A′，B′．

（1）求m的值；
（2）求抛物线E2所表示的二次函数的表达式；
（3）在第一象限内，抛物线E1上是否存在点Q，使得以点Q、B、B′为顶点的三角形为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

【题目】如图所示：

(1)折叠数轴，若1表示的点与-1表示的点重合，则-2表示的点与数 表示的点重合；

(2)折叠数轴，若-1表示的点与5表示的点重合，则4表示的点与 表示的点重合；

(3)已知数轴上点A表示的数是-1，点B表示的数是2，若点A以每秒1个单位长度的速度在数轴上移动，点B以每秒2个单位长度的速度在数轴上移动，且点A始终在点B的左侧，求经过几秒时，A、B两点的距离为6个单位长度.

【题目】在学习了数轴后，小亮决定对数轴进行变化应用：

（1）应用一：已知点A在数轴上表示为，数轴上任意一点B表示的数为，则AB两点的距离可以表示为 ；应用这个知识，请写出当 时，有最小值为 .

（2）应用二：从数轴上取下一个单位长度的线段，第一次剪掉原长的，第二次剪掉剩下的，依次类推，每次都剪掉剩下的，则剪掉5次后剩下线段长度为 ；应用这个原理，请计算：.

（3）应用三：如图，将一根拉直的细线看作数轴，一个三边长分别为的三角形的顶点与原点重合，边在数轴正半轴上，将数轴正半轴的线沿的顺序依次缠绕在三角形的边上，负半轴的线沿的顺序依次缠绕在三角形的边上.

①如果正半轴的线缠绕了5圈，负半轴的线缠绕了3圈，求绕在点上的所有数之和；

②如果正半轴的线不变，将负半轴的线拉长一倍，即原线上的点的位置对应着拉长后的数，并将三角形向正半轴平移一个单位后再开始绕，求绕在点且绝对值不超过100的所有数之和.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网