Question

【题目】在□ABCD中，AE是BC边上的高，AB=10，AE=6，tan∠CAE=，则□ABCD的面积为_____．

Answer 1

【答案】36或60

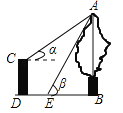
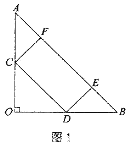
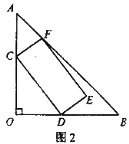
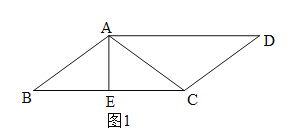
【解析】分析：分两种情况讨论：①E在线段BC上，如图1，②E在BC的延长线上，如图2．分别利用勾股定理和锐角三角函数的定义解答即可．

详解：①如图1．∵AB=10，AE=6，∴BE=8．

∵tan∠CAE=，∴，解得：CE=2，∴BC=BE+CE=10，∴□ABCD的面积=BC×AE=10×6=60；

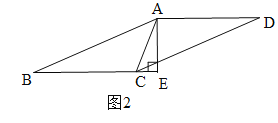
②如图2．∵AB=10，AE=6，∴BE=8．

∵tan∠CAE=，∴，解得：CE=2，∴BC=BE－CE=6，∴□ABCD的面积=BC×AE=6×6=36．

综上所述：□ABCD的面积为36或60．

故答案为：36或60．