题目内容
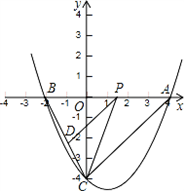
如图,抛物线y=ax2+bx-4与x轴交于A(4,0)、B( -2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
-2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BD·BC;
(3)当△PCD的面积最大时,求点P的坐标.
 -2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
-2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BD·BC;
(3)当△PCD的面积最大时,求点P的坐标.
解:(1)由题意,得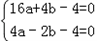 ,解得
,解得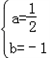 ,
,
∴抛物线的解析式为y=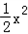 -x-4;
-x-4;
(2)设点P运动到点(x,0)时,有BP2=BD·BC,
令x=0时,则y=-4,∴点C的坐标为(0,-4).
∵PD∥AC,∴△BPD∽△BAC,
∴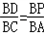 .
.
∵BC=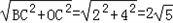 ,
,
AB=6,BP=x-(-2)=x+2.
∴BD=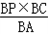 =
= =
=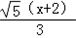 .
.
∵BP2=BDBC,
∴(x+2)2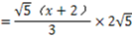
解得x1= ,x2=-2(-2不合题意,舍去),
,x2=-2(-2不合题意,舍去),
∴点P的坐标是( ,0),
,0),
即当点P运动到( ,0)时,BP2=BD·BC;
,0)时,BP2=BD·BC;
(3)∵△BPD∽△BAC,∴ ,
,
∴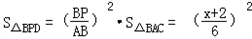 ×
×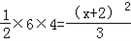 S△BPC
S△BPC
= ×(x+2)×4-
×(x+2)×4-
∵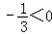 ,
,
∴当x=1时,S△BPC有最大值为3.即点P的坐标为(1,0)时,△PDC的面积最大.
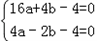 ,解得
,解得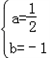 ,
,∴抛物线的解析式为y=
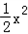 -x-4;
-x-4;(2)设点P运动到点(x,0)时,有BP2=BD·BC,
令x=0时,则y=-4,∴点C的坐标为(0,-4).
∵PD∥AC,∴△BPD∽△BAC,
∴
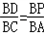 .
.∵BC=
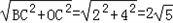 ,
,AB=6,BP=x-(-2)=x+2.
∴BD=
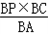 =
= =
=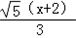 .
.∵BP2=BDBC,
∴(x+2)2
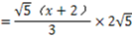
解得x1=
 ,x2=-2(-2不合题意,舍去),
,x2=-2(-2不合题意,舍去),∴点P的坐标是(
 ,0),
,0),即当点P运动到(
 ,0)时,BP2=BD·BC;
,0)时,BP2=BD·BC;(3)∵△BPD∽△BAC,∴
 ,
,∴
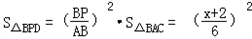 ×
×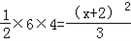 S△BPC
S△BPC=
 ×(x+2)×4-
×(x+2)×4-
∵
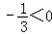 ,
,∴当x=1时,S△BPC有最大值为3.即点P的坐标为(1,0)时,△PDC的面积最大.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目




