题目内容
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④OA(CP-CD)=AP•CD,正确的结论有( )个.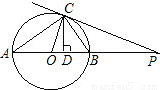
A.1
B.2
C.3
D.4
【答案】分析:①证明△PBC∽△PCA,即可得到结论,这实际上是圆的切割线定理,正确;
②根据切线的性质定理,得OC⊥PC,再根据直角三角形的面积公式即可证明结论,正确;
③根据直角三角形的射影定理,得OC2=OD•OP,再根据OA=OC,即可证明结论,正确;
④根据△APC的面积分析,显然错误.
解答:解:①∵PC与⊙O相切于点C,∴∠PCB=∠A,∠P=∠P
∴△PBC∽△PCA,
∴PC2=PA•PB
②∵OC⊥PC,
∴PC•OC=OP•CD
③∵CD⊥AB,OC⊥PC,
∴OC2=OD•OP,
∵OA=OC
∴OA2=OD•OP
④∵ AP•CD=
AP•CD= •OC•CP+
•OC•CP+ OA•CD,OA=OC
OA•CD,OA=OC
∴OA(CP-CD)=AP•CD
所以正确的有①,②,③④,共4个.
故选D.
点评:综合运用切割线定理、射影定理、不同的角度表示同一个三角形的面积.
②根据切线的性质定理,得OC⊥PC,再根据直角三角形的面积公式即可证明结论,正确;
③根据直角三角形的射影定理,得OC2=OD•OP,再根据OA=OC,即可证明结论,正确;
④根据△APC的面积分析,显然错误.
解答:解:①∵PC与⊙O相切于点C,∴∠PCB=∠A,∠P=∠P
∴△PBC∽△PCA,
∴PC2=PA•PB
②∵OC⊥PC,
∴PC•OC=OP•CD
③∵CD⊥AB,OC⊥PC,
∴OC2=OD•OP,
∵OA=OC
∴OA2=OD•OP
④∵
 AP•CD=
AP•CD= •OC•CP+
•OC•CP+ OA•CD,OA=OC
OA•CD,OA=OC∴OA(CP-CD)=AP•CD
所以正确的有①,②,③④,共4个.
故选D.
点评:综合运用切割线定理、射影定理、不同的角度表示同一个三角形的面积.

练习册系列答案
相关题目
 6、如图,把一块含有30°的直角尺ACB绕点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则∠BCD的度数是
6、如图,把一块含有30°的直角尺ACB绕点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则∠BCD的度数是 在第一象限内的图象如图,点M是图像上一点,MP垂
在第一象限内的图象如图,点M是图像上一点,MP垂
 如图,把一块含有30°的直角尺ACB绕点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则∠BCD的度数是________.
如图,把一块含有30°的直角尺ACB绕点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则∠BCD的度数是________.
