题目内容
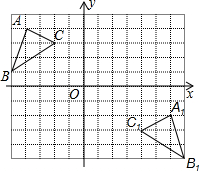如图所示，在对△ABC依次进行轴对称和平移两种变换后得到△A1A1C1．（1）在坐标系内画出轴对称变换的图形，并说明两次变换的步骤．
（2）设点P（a，b）为△ABC的边AB上任一点，依次写出这两次变换后点P对应的坐标．
分析：（1）结合两三角形的位置关系，可得出先将△ABC关于y轴对称，然后向右平移4个单位，向下平移5个单位，即可得出△A1A1C1．
（2）根据关于y轴对称的点的坐标，纵坐标相等，横坐标互为相反数，结合平移的特点即可得出两次变换后点P对应的坐标．
（2）根据关于y轴对称的点的坐标，纵坐标相等，横坐标互为相反数，结合平移的特点即可得出两次变换后点P对应的坐标．
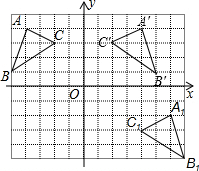
解答：解：轴对称变换后的图形如图所示：△A'B'C'．
变换的步骤为：将△ABC关于y轴对称，然后向右平移4个单位，向下平移5个单位，
．
（2）点P关于y轴对称的点的坐标为（-a，b），
再向右平移4个单位，向下平移5个单位，可得点P的对应点坐标为（-a+5，b-4）．
变换的步骤为：将△ABC关于y轴对称，然后向右平移4个单位，向下平移5个单位，
．（2）点P关于y轴对称的点的坐标为（-a，b），
再向右平移4个单位，向下平移5个单位，可得点P的对应点坐标为（-a+5，b-4）．
点评：本题考查了平移变换及轴对称变换的特点，解答本题的关键是仔细观察变换前后的图形，另外要求同学们掌握关于y轴对称的点的坐标．
练习册系列答案
相关题目
在课外活动中，小明发明了一个在直角三角形中画锐角的平分线的方法，他的方法是：如图所示，在斜边AB上取一点E，使BE=BC，过点E作ED⊥AB，交AC于D，那么BD就是∠ABC的平分线，你认为对吗？为什么？
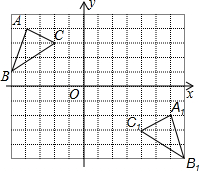如图所示，在对△ABC依次进行轴对称和平移两种变换后得到△A1A1C1．