题目内容
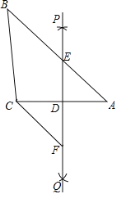
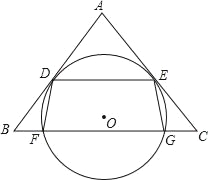
【题目】如图,O是△ABC内一点,⊙O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC.连接 DF、EG.
(1)求证:AB=AC.
(2)已知 AB=5,BC=6.求四边形DFGE是矩形时⊙O的半径.
【答案】(1)证明见解析;(2)四边形DFGE是矩形时⊙O的半径为![]() .
.
【解析】
(1)由切线长定理可知AD=AE,易得∠ADE=∠AED,因为DE∥BC,由平行线的性质得∠ADE=∠B,∠AED=∠C,可得∠B=∠C,易得AB=AC;
(2)如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设⊙O半径为r,由△AOD∽△ABN得![]() ,得到AD=
,得到AD=![]() r,再由△GBD∽△ABN得
r,再由△GBD∽△ABN得![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
(1)证明:∵AD、AE是⊙O的切线,
∴AD=AE,
∴∠ADE=∠AED,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠B=∠C,
∴AB=AC;
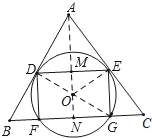
(2)如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设⊙O半径为r,
∵四边形DFGE是矩形,
∴∠DFG=90°,
∴DG是⊙O直径,
∵⊙O与AB、AC分别相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵OD=OE.
∴AN平分∠BAC,∵AB=AC,
∴AN⊥BC,BN=![]() BC=3,
BC=3,
在Rt△ABN中,AN=![]() ,
,
∵OD⊥AB,AN⊥BC,
∴∠ADO=∠ANB=90°,
∵∠OAD=∠BAN,
∴△AOD∽△ABN,
∴![]() ,即
,即![]() ,
,
∴AD=![]() r,
r,
∴BD=AB﹣AD=5﹣![]() r,
r,
∵OD⊥AB,
∴∠GDB=∠ANB=90°,
∵∠B=∠B,
∴△GBD∽△ABN,
∴![]() ,即
,即![]() ,
,
∴r=![]() ,
,
∴四边形DFGE是矩形时⊙O的半径为![]()

练习册系列答案
相关题目