题目内容
(本题满分7分)如图,已知在Rt△ABC,AB=AC,∠BAC=90°,过A的任一条直线AN,BD⊥AN于D,CE⊥AN于E。
⑴求证:DE=BD-CE
⑵如将直线AN绕A点沿顺时针方向旋转,使它不经过△ABC的内部,再作BD⊥AN于D,CE⊥AN于E,那么DE、DB、CE之间存在等量关系吗?若存在,请证明你的结论?

(1)证明:∵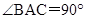 ,,BD⊥AN,∴
,,BD⊥AN,∴ ,
,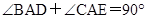 ,∴
,∴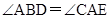 ,∵BD⊥AN,CE⊥AN,∴
,∵BD⊥AN,CE⊥AN,∴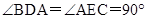 ,在△ABD与△CAE中,
,在△ABD与△CAE中,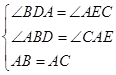 ,∴△ABD≌△CAE,∴
,∴△ABD≌△CAE,∴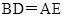 ,
,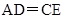 ,∵
,∵ ,∴
,∴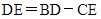
(2)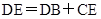
解析试题分析:(1)先通过证明三角形全等,从而证明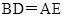 ,
,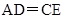 ,所以
,所以 ,等量代换,可得
,等量代换,可得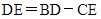
(2)∵BD⊥AN,CE⊥AN,∴ ,∴
,∴ ,∵
,∵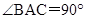 ,∴
,∴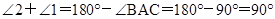 ,∴
,∴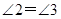 ,在△BDA和△AEC中,
,在△BDA和△AEC中,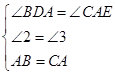 ,∴△BDA≌△AEC,∴
,∴△BDA≌△AEC,∴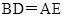 ,
,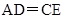 ,∴
,∴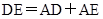
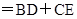
考点:全等三角形的应用
点评:本题难度一般,通过全等三角形的性质,证明两个三角形全等,进而证明对应边相等。全等三角形是考试必考部分,学生做此类题目时需要谨慎小心,依据全等三角形的各类判定依据进行推导

练习册系列答案
相关题目
.(本题满分5分)如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
 |
1.若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为 cm.
2.由题(1)的启发,请你借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?


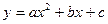 交
交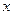 轴于
轴于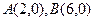 两点,交
两点,交 轴于点
轴于点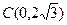 .
.
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交