题目内容
如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,正方形ABCD的四个顶点分别在这四条直线上,且正方形ABCD的面积是25。
(1)连结EF,证明△ABE、△FBE、△EDF、△CDF的面积相等。
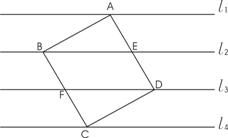
(2)求h的值。
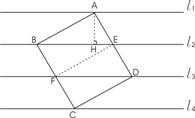 |
解:连结EF
∵l1∥l2∥l3∥l4,且四边形ABCD是正方形
∴BE∥FD,BF∥ED
∴四边形EBFD为平行四边形
∴BE=FD
又∵l1、l2、l3和l4之间的距离为h
∴S△ABE=![]() BE?h,S△FBE=
BE?h,S△FBE=![]() BE?h,S△EDF=
BE?h,S△EDF=![]() FD?h,S△CDF=
FD?h,S△CDF=![]() FD?h
FD?h
∴S△ABE= S△FBE= S△EDF= S△CDF)
(2)过A点作AH⊥BE于H点。
方法一:∵S△ABE= S△FBE= S△EDF= S△CDF
又∵ 正方形ABCD的面积是25
∴![]() ,且AB=AD=5
,且AB=AD=5
又∵l1∥l2∥l3∥l4
∴E、F分别是AD与BC的中点
∴AE=![]() AD=
AD=![]()
∴在Rt△ABE中,
BE=![]()
又∵AB?AE=BE?AH
∴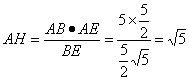
方法二:不妨设BE=FD=x (x>0)
则S△ABE= S△FBE= S△EDF= S△CDF=![]()
又∵正方形ABCD的面积是25,
∴S△ABE=![]() ,且AB=5
,且AB=5
则![]()
又∵在Rt△ABE中:AE=![]()
又∵∠BAE=90o,AH⊥BE
∴Rt△ABE∽Rt△HAE
∴![]() ,即
,即![]()
变形得:![]()
把①两边平方后代入②得:![]()
解方程③得![]() (
(![]() 舍去)
舍去)
把![]() 代入①得:
代入①得:![]()

练习册系列答案
相关题目
 22、某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则以下判断错误的是( )
22、某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则以下判断错误的是( )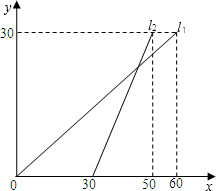 的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
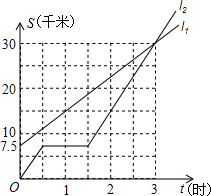 如图,l1、l2分别表示步行者与骑自行车在同一路上行驶的路程S与时间t的关系.
如图,l1、l2分别表示步行者与骑自行车在同一路上行驶的路程S与时间t的关系. 如图,l1,l2分别表示一种白炽灯和一种节能灯的费用y与照明时间x(h)的函数图象,假设两种灯的使用寿命都是2000h,照明效果一样.(费用=灯的售价+电费,单位:元)
如图,l1,l2分别表示一种白炽灯和一种节能灯的费用y与照明时间x(h)的函数图象,假设两种灯的使用寿命都是2000h,照明效果一样.(费用=灯的售价+电费,单位:元)