题目内容
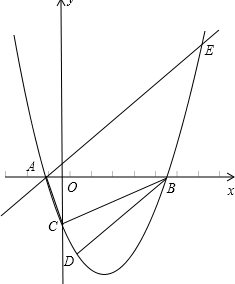 设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90度.
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90度.(1)求m的值;
(2)求抛物线的解析式,并验证点D(1,-3)是否在抛物线上;
(3)已知过点A的直线y=x+1交抛物线于另一点E.问:在x轴上是否存在点P,使以点P、B、D为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标;若不存在,请说明理由.
分析:(1)根据抛物线的解析式可知OC=2,由于∠ACB=90°,可根据射影定理求出OB的长,即可得出B点的坐标,也就得出了m的值.然后根据A,B,C三点的坐标,用待定系数法可求出抛物线的解析式.
(2)将D点的坐标代入(1)得出的抛物线的解析式中,即可判断出D是否在抛物线上.
(3)本题要分情况进行讨论,如果过E作x轴的垂线,不难得出∠DBx=135°,而∠ABE是个钝角但小于135°,因此P点只能在B点左侧.可分两种情况进行讨论:
①∠DPB=∠ABE,即△DBP∽△EAB,可得出BP:AP=BD:AE,可据此来求出P点的坐标.
②∠PDB=∠ABE,即△DBP∽△BAE,方法同①,只不过对应的成比例线段不一样.
综上所述可求出符合条件的P点的值.
(2)将D点的坐标代入(1)得出的抛物线的解析式中,即可判断出D是否在抛物线上.
(3)本题要分情况进行讨论,如果过E作x轴的垂线,不难得出∠DBx=135°,而∠ABE是个钝角但小于135°,因此P点只能在B点左侧.可分两种情况进行讨论:
①∠DPB=∠ABE,即△DBP∽△EAB,可得出BP:AP=BD:AE,可据此来求出P点的坐标.
②∠PDB=∠ABE,即△DBP∽△BAE,方法同①,只不过对应的成比例线段不一样.
综上所述可求出符合条件的P点的值.
解答: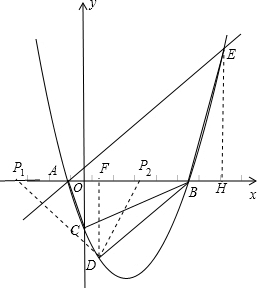 解:(1)令x=0,得y=-2
解:(1)令x=0,得y=-2
∴C(0,-2)
∵∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OA•OB=OC2
∴OB=
=
=4
∴m=4
(2)将A(-1,0),B(4,0)代入y=ax2+bx-2,
解得
,
∴抛物线的解析式为y=
x2-
x-2,
当x=1时,y=
x2-
x-2=-3,
∴点D(1,-3)在抛物线上.
(3)由得
,
∴E(6,7),
过E作EH⊥x轴于H,则H(6,0),
∴AH=EH=7,
∴∠EAH=45°,
作DF⊥x轴于F,则F(1,0),
∴BF=DF=3
∴∠DBF=45°,
∴∠EAH=∠DBF=45°,
∴∠DBH=135°,90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则
=
,
∴BP1=
=
=
∴OP1=4-
=
,
∴P1(
,0);
②若△DBP2∽△BAE,则
=
,
∴BP2=
=
=
∴OP2=
-4=
∴P2(-
,0).
综合①、②,得点P的坐标为:P1(
,0)或P2(-
,0).
 解:(1)令x=0,得y=-2
解:(1)令x=0,得y=-2∴C(0,-2)
∵∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OA•OB=OC2
∴OB=
| OC2 |
| OA |
| 4 |
| 1 |
∴m=4
(2)将A(-1,0),B(4,0)代入y=ax2+bx-2,
解得
|
∴抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
当x=1时,y=
| 1 |
| 2 |
| 3 |
| 2 |
∴点D(1,-3)在抛物线上.
(3)由得
|
|
∴E(6,7),
过E作EH⊥x轴于H,则H(6,0),
∴AH=EH=7,
∴∠EAH=45°,
作DF⊥x轴于F,则F(1,0),
∴BF=DF=3
∴∠DBF=45°,
∴∠EAH=∠DBF=45°,
∴∠DBH=135°,90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则
| BP1 |
| AB |
| BD |
| AE |
∴BP1=
| AB•BD |
| AE |
5×3
| ||
7
|
| 15 |
| 7 |
∴OP1=4-
| 15 |
| 7 |
| 13 |
| 7 |
∴P1(
| 13 |
| 7 |
②若△DBP2∽△BAE,则
| BP2 |
| AE |
| BD |
| AB |
∴BP2=
| AE•BD |
| AB |
7
| ||||
| 5 |
| 42 |
| 5 |
∴OP2=
| 42 |
| 5 |
| 22 |
| 5 |
∴P2(-
| 22 |
| 5 |
综合①、②,得点P的坐标为:P1(
| 13 |
| 7 |
| 22 |
| 5 |
点评:本题着重考查了待定系数法求二次函数解析式、相似三角形的判定和性质等知识点,综合性较强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
 ACB=90度.
ACB=90度. ,0),与y轴交于点C(0,-2),且∠ACB=90度.
,0),与y轴交于点C(0,-2),且∠ACB=90度.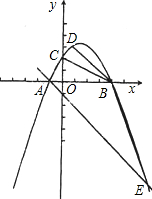 设抛物线y=ax2+bx+c与x轴交于两个不同的点A(-l,0)、B(4,0),与y轴交于点C(0,2).
设抛物线y=ax2+bx+c与x轴交于两个不同的点A(-l,0)、B(4,0),与y轴交于点C(0,2). m2-mb+n),其中 a,b,c,m,n为实数,且a,m不为0.
m2-mb+n),其中 a,b,c,m,n为实数,且a,m不为0.