题目内容
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.(1)求此抛物线的表达式;
(2)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,
(3)点P是抛物线对称轴上一动点,抛物线上是否存在一点Q,使得以A、B、P、Q为顶点的四边形为平行四边形?如果存在,请直接写出Q点坐标;如果不存在,请说明理由.

【答案】分析:(1)解一元二次方程求出点B、C的坐标,再根据二次函数的对称性求出点A的坐标,然后利用待定系数法求二次函数解析式解答即可;
(2)先表示出BE的长度并求出△ABC的面积,再判定△BEF和△ABC相似,然后根据相似三角形面积的比等于相似比的平方表示出△BEF的面积,再根据等高的三角形的面积的比等于底边的比列式求解即可得到S与m的关系式,然后根据二次函数的最值问题解答即可;
(3)根据平行四边形的性质,分①AB是对角线时,根据二次函数的对称性,点Q是抛物线的顶点时,以A、B、P、Q为顶点的四边形为平行四边形;②AB是边时,根据平行四边形的对边相等先求出点Q的横坐标,然后代入抛物线解析式计算即可得解.
解答:解:(1)由方程x2-10x+16=0得,x1=2,x2=8,
∵点B在x轴的正半轴上,点C在y轴的正半轴上,OB<OC,
∴点B的坐标为(2,0),点C的坐标为(0,8),
∵抛物线的对称轴是直线x=-2,
∴点A的坐标是(-6,0),
∵点A、B、C都在抛物线y=ax2+bx+c上,
∴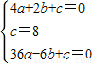 ,
,
解得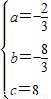 ,
,
∴此抛物线的表达式为y=- x2-
x2- x+8;
x+8;
(2)∵A(-6,0),B(2,0),AE的长为m,
∴AB=2-(-6)=2+6=8,BE=8-m,
S△ABC= ×8×8=32,
×8×8=32,
∵EF∥AC,
∴△BEF∽△ABC,
∴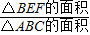 =(
=(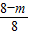 )2,
)2,
∴△BEF的面积=32×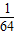 (8-m)2=
(8-m)2= (8-m)2,
(8-m)2,
由EF∥AC可得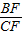 =
=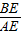 =
=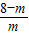 ,
,
等高的三角形的面积的比等于底边的比可得: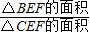 =
=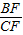 =
=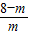 ,
,
∴S=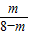 ×
× (8-m)2=
(8-m)2= m(8-m)=-
m(8-m)=- m2+4m(0<m<8),
m2+4m(0<m<8),
又∵S=- m2+4m=-
m2+4m=- (m2-8m+16)+8=-
(m2-8m+16)+8=- (m-4)2+8,
(m-4)2+8,
∴当m=4时,S有最大值,最大值是8,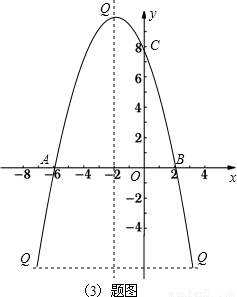
此时,OE=6-4=2,
∴点E的坐标为(-2,0);
(3)存在点Q(-2,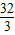 )或(6,-32)或(-10,-32),使得以A、B、P、Q为顶点的四边形为平行四边形.
)或(6,-32)或(-10,-32),使得以A、B、P、Q为顶点的四边形为平行四边形.
理由如下:①很明显,当AB是对角线时,点Q在顶点时,以A、B、P、Q为顶点的四边形可以为平行四边形,
此时y=- x2-
x2- x+8=-
x+8=- (x+2)2+
(x+2)2+ +8=-
+8=- (x+2)2+
(x+2)2+ ,
,
∴顶点坐标为(-2,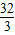 ),
),
即点Q的坐标为(-2,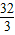 ),
),
②当AB为边时,∵AB=8(已求),
∴PQ=8,
∵点P在对称轴x=-2上,
∴点Q的横坐标为6或-10,
当横坐标为6时,y=- ×62-
×62- ×6+8=-32,
×6+8=-32,
当横坐标是-10时,y=- ×(-10)2-
×(-10)2- ×(-10)+8=-32,
×(-10)+8=-32,
∴点Q的坐标为(6,-32)或(-10,-32),
故存在点Q(-2,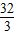 )或(6,-32)或(-10,-32),使得以A、B、P、Q为顶点的四边形为平行四边形.
)或(6,-32)或(-10,-32),使得以A、B、P、Q为顶点的四边形为平行四边形.
点评:本题综合考查了二次函数,主要有一元二次方程的解法,待定系数法求二次函数解析式,相似三角形面积的比等于相似比的平方的性质,等高的三角形的面积的比等于底边的比,以及平行四边形的对边相等的性质,(3)注意要分AB是对角线与边两种情况讨论.
(2)先表示出BE的长度并求出△ABC的面积,再判定△BEF和△ABC相似,然后根据相似三角形面积的比等于相似比的平方表示出△BEF的面积,再根据等高的三角形的面积的比等于底边的比列式求解即可得到S与m的关系式,然后根据二次函数的最值问题解答即可;
(3)根据平行四边形的性质,分①AB是对角线时,根据二次函数的对称性,点Q是抛物线的顶点时,以A、B、P、Q为顶点的四边形为平行四边形;②AB是边时,根据平行四边形的对边相等先求出点Q的横坐标,然后代入抛物线解析式计算即可得解.
解答:解:(1)由方程x2-10x+16=0得,x1=2,x2=8,
∵点B在x轴的正半轴上,点C在y轴的正半轴上,OB<OC,
∴点B的坐标为(2,0),点C的坐标为(0,8),
∵抛物线的对称轴是直线x=-2,
∴点A的坐标是(-6,0),
∵点A、B、C都在抛物线y=ax2+bx+c上,
∴
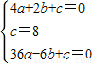 ,
,解得
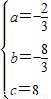 ,
,
∴此抛物线的表达式为y=-
 x2-
x2- x+8;
x+8;(2)∵A(-6,0),B(2,0),AE的长为m,
∴AB=2-(-6)=2+6=8,BE=8-m,
S△ABC=
 ×8×8=32,
×8×8=32,∵EF∥AC,
∴△BEF∽△ABC,
∴
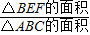 =(
=(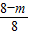 )2,
)2,∴△BEF的面积=32×
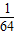 (8-m)2=
(8-m)2= (8-m)2,
(8-m)2,由EF∥AC可得
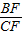 =
=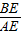 =
=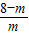 ,
,等高的三角形的面积的比等于底边的比可得:
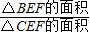 =
=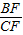 =
=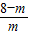 ,
,∴S=
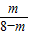 ×
× (8-m)2=
(8-m)2= m(8-m)=-
m(8-m)=- m2+4m(0<m<8),
m2+4m(0<m<8),又∵S=-
 m2+4m=-
m2+4m=- (m2-8m+16)+8=-
(m2-8m+16)+8=- (m-4)2+8,
(m-4)2+8,∴当m=4时,S有最大值,最大值是8,

此时,OE=6-4=2,
∴点E的坐标为(-2,0);
(3)存在点Q(-2,
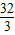 )或(6,-32)或(-10,-32),使得以A、B、P、Q为顶点的四边形为平行四边形.
)或(6,-32)或(-10,-32),使得以A、B、P、Q为顶点的四边形为平行四边形.理由如下:①很明显,当AB是对角线时,点Q在顶点时,以A、B、P、Q为顶点的四边形可以为平行四边形,
此时y=-
 x2-
x2- x+8=-
x+8=- (x+2)2+
(x+2)2+ +8=-
+8=- (x+2)2+
(x+2)2+ ,
,∴顶点坐标为(-2,
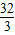 ),
),即点Q的坐标为(-2,
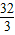 ),
),②当AB为边时,∵AB=8(已求),
∴PQ=8,
∵点P在对称轴x=-2上,
∴点Q的横坐标为6或-10,
当横坐标为6时,y=-
 ×62-
×62- ×6+8=-32,
×6+8=-32,当横坐标是-10时,y=-
 ×(-10)2-
×(-10)2- ×(-10)+8=-32,
×(-10)+8=-32,∴点Q的坐标为(6,-32)或(-10,-32),
故存在点Q(-2,
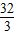 )或(6,-32)或(-10,-32),使得以A、B、P、Q为顶点的四边形为平行四边形.
)或(6,-32)或(-10,-32),使得以A、B、P、Q为顶点的四边形为平行四边形.点评:本题综合考查了二次函数,主要有一元二次方程的解法,待定系数法求二次函数解析式,相似三角形面积的比等于相似比的平方的性质,等高的三角形的面积的比等于底边的比,以及平行四边形的对边相等的性质,(3)注意要分AB是对角线与边两种情况讨论.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=