题目内容
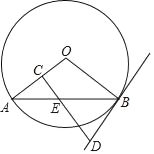
【题目】如图,AB是⊙O的直径,弦CD⊥AB ,垂足为H,连接AC,过![]() 上一点E作 EG∥AC 交CD的延长线于点G,连接AE交CD于点F,且EG=FG .
上一点E作 EG∥AC 交CD的延长线于点G,连接AE交CD于点F,且EG=FG .
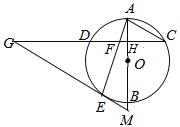
(1)求证:EG是 ⊙O 的切线;
(2)延长AB交GE的延长线于点M ,若tanG=![]() ,AH=2,求 EM 的值.
,AH=2,求 EM 的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】分析:(1)欲证明EG是⊙O的切线只要证明EG⊥OE即可;
(2)连接OC.设⊙O的半径为r.在Rt△OCH中,利用勾股定理求出r,证明△AHC∽△MEO,可得![]() ,由此即可解决问题.
,由此即可解决问题.
详解:(1)如图,连接OE,
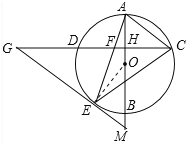
∵GF=GE,
∴∠GFE=∠GEF=∠AFH,
∵OA=OE,
∴∠OAE=∠OEA,
∵AB⊥CD,
∴∠AFH+∠FAH=90°,
∴∠GEF+∠AEO=90°,
∴∠GEO=90°
∴GE⊥OE,
∴EG是⊙O的切线;
(2)如图,连接OC.
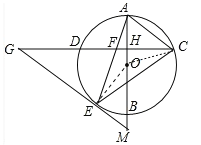
设⊙O的半径为r,
在Rt△AHC中,tan∠ACH=tan∠G=![]() ,
,
∵AH=2,
∴HC=4,
在Rt△HOC中,
∵OC=r,OH=r-2,HC=4,
∴![]() ,
,
∴r=5,
∵GM∥AC,
∴∠CAH=∠M,
∵∠OEM=∠AHC,
∴△AHC∽△MEO
∴![]() ,
,
∴![]() ,
,
∴EM=![]() .
.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目