��Ŀ����
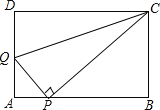
����Ŀ����ͼ��������ABCD�У�![]() ��
��![]() ��
��![]() �ֱ�������ABCD�������Խ��߳��ͱ߳�����ʱ���ǰѹ���
�ֱ�������ABCD�������Խ��߳��ͱ߳�����ʱ���ǰѹ���![]() ��������
��������![]() ����һԪ���η��̳�Ϊ����ϵһԪ���η������������������⣺
����һԪ���η��̳�Ϊ����ϵһԪ���η������������������⣺
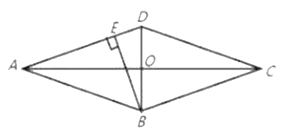
��1����գ�����![]() ��
��![]() ʱ��
ʱ��![]() ��
��
���ú�![]() ��
��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ֵ��
ֵ��![]() ��
��
��2����֤������![]() ������ϵһԪ���η�����
������ϵһԪ���η�����![]() ����ʵ������
����ʵ������
��3����![]() ������ϵһԪ���η�����
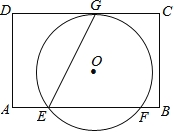
������ϵһԪ���η�����![]() ��һ�����������ε������25��BE������ABCD��AD���ϵĸߣ���BE��ֵ��
��һ�����������ε������25��BE������ABCD��AD���ϵĸߣ���BE��ֵ��
���𰸡���1����5����![]() ����2������������3��
����2������������3��![]()
��������
��1�����ͼ�Σ��������εĶԽ�����ƽ���Լ����ɶ������ɵõ����ۣ�
��2�����������ϣ�1���ТڵĽ��ۼ��ɽ�����⣻
��3�����ݷ��̸��Ķ���ó�m��n��t�Ĺ�ϵ����ϣ�1���ТڵĽ��۽��л����ٸ������������25�����ɵó�t��ֵ�������ó����ۣ�
��1���ٵ�m=6��n=8ʱ��AO=4��OB=3����t=AB=![]() =5��
=5��
�ڡ�AO=![]() ��OB=
��OB=![]() ����t2=AB2=
����t2=AB2=![]() ��
��
�ʴ�Ϊ��5��![]() ��
��
��2��![]()
���a=m��b=![]() t��c=n����
t��c=n����![]() ��
��
��![]() ����
����![]()
![]() �������
�������![]() ������ϵһԪ���η�����
������ϵһԪ���η�����![]() ����ʵ������
����ʵ������
��3����![]() ������ϵһԪ���η�����
������ϵһԪ���η�����![]() ��һ��������
��һ��������![]() ����
����![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
�����������25����![]() ����
����![]() ����ã�
����ã�![]() ����
����![]() ����
����![]() ��
��

����Ŀ�������г�����Խ��Խ�ܵ����ǵ�ϲ��������Ʒ�Ƶ�ɽ�����г����Ͷ���г���˳�糵�о�Ӫ��![]() �ͳ�ȥ��6�·������ܶ�Ϊ3.2��Ԫ�����꾭������������
�ͳ�ȥ��6�·������ܶ�Ϊ3.2��Ԫ�����꾭������������![]() �ͳ�ÿ�����ۼ۱�ȥ������400Ԫ��������6�·���ȥ��6�·�������
�ͳ�ÿ�����ۼ۱�ȥ������400Ԫ��������6�·���ȥ��6�·�������![]() �ͳ�������ͬ�������6�·�
�ͳ�������ͬ�������6�·�![]() �ͳ������ܶ��ȥ��6�·������ܶ�����
�ͳ������ܶ��ȥ��6�·������ܶ�����![]() ��
��
![]() ��
��![]() �����ͺų��Ľ��������ۼ۸����
�����ͺų��Ľ��������ۼ۸����
|
| |
�����۸�Ԫ | 1100 | 1400 |
���ۼ۸�Ԫ | ��������ۼ۸� | 2400 |
��1�������6�·�![]() �ͳ�ÿ�����ۼ۶���Ԫ��
�ͳ�ÿ�����ۼ۶���Ԫ��
��2���ó��мƻ�7�·��½�һ��![]() �ͳ���
�ͳ���![]() �ͳ���50������
�ͳ���50������![]() �ͳ��Ľ�������������
�ͳ��Ľ�������������![]() �ͳ�������������Ӧ��ν�������ʹ������������ࣿ
�ͳ�������������Ӧ��ν�������ʹ������������ࣿ