题目内容
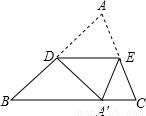
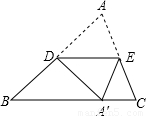
 如图,△ABC沿DE折叠后,点A落在BC边上的A′处,若点D为AB边的中点,∠B=50°,则∠BDA′的度数为( )
如图,△ABC沿DE折叠后,点A落在BC边上的A′处,若点D为AB边的中点,∠B=50°,则∠BDA′的度数为( )分析:由折叠的性质可知AD=A′D,再根据中点的性质得AD=BD=A′D,根据等腰三角形的性质可得∠DA′B=∠B=50°,从而求解∠BDA'的度数.
解答:解:由折叠的性质知,AD=A′D,
∵点D为AB边的中点,
∴AD=BD,
∴BD=A′D,
∴∠DA′B=∠B=50°,
∴∠BDA′=180°-2∠B=80°.
故选D.
∵点D为AB边的中点,
∴AD=BD,
∴BD=A′D,
∴∠DA′B=∠B=50°,
∴∠BDA′=180°-2∠B=80°.
故选D.
点评:本题考查了翻折变换的知识,解答本题的关键是根据翻折变换的性质:翻折前后对应边相等,得出△BDA'是等腰三角形,此题难度一般.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
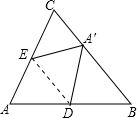 如图,△ABC沿DE折叠后,点A落在BC边上的A′处,若点D为AB的中点,∠B=53°,则∠BDA′的度数为
如图,△ABC沿DE折叠后,点A落在BC边上的A′处,若点D为AB的中点,∠B=53°,则∠BDA′的度数为 (2007•海南)如图,△ABC沿DE折叠后,点A落在BC边上的A′处,若点D为AB边的中点,∠B=50°,则∠BDA′的度数为
(2007•海南)如图,△ABC沿DE折叠后,点A落在BC边上的A′处,若点D为AB边的中点,∠B=50°,则∠BDA′的度数为