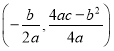题目内容
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() ,直线
,直线![]() 是抛物线的对称轴,在直线
是抛物线的对称轴,在直线![]() 右侧的抛物线上有一动点
右侧的抛物线上有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
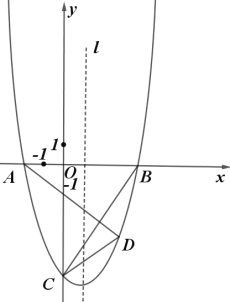
(1)求抛物线的函数表达式;
(2)若点![]() 在
在![]() 轴的下方,当
轴的下方,当![]() 的面积是
的面积是![]() 时,求
时,求![]() 的面积;
的面积;
(3)在(2)的条件下,点![]() 是
是![]() 轴上一点,点
轴上一点,点![]() 是抛物线上一动点,是否存在点
是抛物线上一动点,是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为一边的四边形是平行四边形,若存在,求出点
为一边的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]() 或
或![]() .
.
【解析】
(1)直接利用待定系数法可求得函数解析式;
(2)先求出函数的对称轴和直线BC的函数表达式,过D作DE⊥OB交OB于点F,交BC于点E,用式子表示出![]() 的面积从而求出D的坐标,进一步可得
的面积从而求出D的坐标,进一步可得![]() 的面积;
的面积;
(3)根据平行四边形的性质得到![]() ,结合对称轴和点D坐标易得点N的坐标.
,结合对称轴和点D坐标易得点N的坐标.
解:(1)∵OA=2,OB=4,
∴A(-2,0),B(4,0),
将A(-2,0),B(4,0)代入![]() 得:
得:
![]() ,
,
解得:![]()
∴抛物线的函数表达式为:![]() ;
;
(2)由(1)可得抛物线![]() 的对称轴l:
的对称轴l:![]() ,
,![]() ,
,
设直线BC:![]() ,
,
可得:![]()
解得![]() ,
,
∴直线BC的函数表达式为:![]() ,
,
如图1,过D作DE⊥OB交OB于点F,交BC于点E,
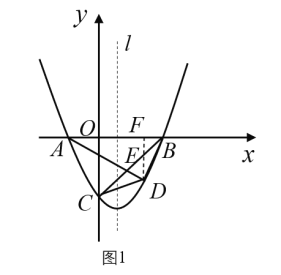
设![]() ,则
,则![]() ,
,
∴![]() ,
,
由题意可得![]()
整理得![]()
解得![]() (舍去),
(舍去),![]()
∴![]() ,
,
∴![]()
∴![]()
![]()
![]() ;
;
(3)存在
由(1)可得抛物线![]() 的对称轴l:
的对称轴l:![]() ,由(2)知
,由(2)知![]() ,
,
①如图2
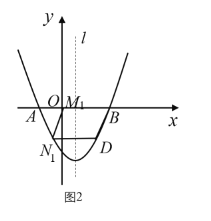
当![]() 时,四边形BDNM即为平行四边形,
时,四边形BDNM即为平行四边形,
此时MB=ND=4,点M与点O重合,四边形BDNM即为平行四边形,
∴由对称性可知N点横坐标为-1,将x=-1代入![]()
解得![]()
∴此时![]() ,四边形BDNM即为平行四边形.
,四边形BDNM即为平行四边形.
②如图3
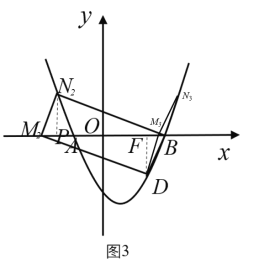
当![]() 时,四边形BDMN为平行四边形,
时,四边形BDMN为平行四边形,
过点N做NP⊥x轴,过点D做DF⊥x轴,由题意可得NP=DF
∴此时N点纵坐标为![]()
将y=![]() 代入
代入![]() ,
,
得![]() ,解得:
,解得:![]()
∴此时![]() 或
或![]() ,四边形BDMN为平行四边形.
,四边形BDMN为平行四边形.
综上所述, ![]() 或
或![]() 或
或![]() .
.

【题目】某校准备组织师生共60人,从甲地乘动车前往乙地参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
甲地 | 乙地 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)求参加活动的教师和学生各有多少人?
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,后续前往的教师和学生均购买二等座票.设提早前往的教师有![]() 人,购买一、二等座票全部费用为
人,购买一、二等座票全部费用为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若购买一、二等座票全部费用不多于1030元,则提早前往的教师最多只能有多少人?
【题目】某体育器材专卖柜经销A、B两种器材,A种器材每件进价350元,售价480元;B种器材每件进价200元,售价300元.
(1)该专卖柜计划用8000元去购进A、B两种器材若干件.
①若购进A种器材x件,B种器材y件,所获利润w元,请写出w与x之间满足的函数关系式;
②怎样购进才能使专卖柜经销这两种器材所获利润最大(其中A种器材不少于7件)?
(2)在“五·一”期间,该专卖柜对A、B两种器材进行如下优惠促销活动:
一次性购物总金额 | 优惠措施 |
不超过3000元 | 不优惠 |
超过3000元不超过4000元 | 售价打八折 |
超过4000元 | 售价打七折 |
促销活动期间:甲学校去该专卖柜购买A种器材付款2688元;乙学校去该专卖柜购买B种器材付款2100元,求丙学校决定一次性购买甲学校和乙学校购买的同样多的器材需付款多少元?