题目内容
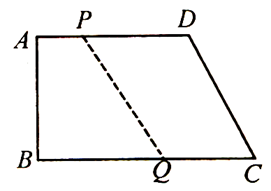
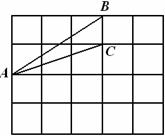
在梯形ABCD中,AD∥BC,AB=CD,BC=4AD,AD= ,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF= .
,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF= .
 ,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF= .
,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF= .
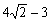
试题分析:首先理解题意,得出此题应该分两种情况进行分析,分别是AB=AE,AB=BE,从而得到最后答案.
根据已知条件可得,
AB=(BC-AD)÷2÷cosB=3.
①当AB=AE时,
∠B=45°,∠AEB=45°,AE=AB=3,
则在Rt△ABE中,BE=3
 ,
,故EC=4
 -3
-3 =
=
易得△FEC为等腰直角三角形,
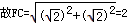
②当AB=BE时,
∵∠B+∠BAE=45°+∠CEF,∠B=45°,
∴∠CEF=∠AEB,
∵∠B=∠C,
∴△ABE∽△ECF,
易得△FEC为等腰直角三角形,
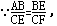
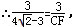
∴CF=4
 -3;
-3;△ABE∽△FCE,
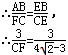
∴CF=4
 -3.
-3.点评:本题知识点多,综合性强,难度较大,是中考常见题,一般在选择题或填空题的最后一题出现.

练习册系列答案
相关题目
 中,
中, 4,
4,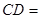 13,
13, 12,∠
12,∠
 90°,∠
90°,∠ 135°, 四边形
135°, 四边形

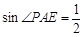 ③HP//AE ④HF=1 ⑤
③HP//AE ④HF=1 ⑤

 为1,按上述方法所作的正方形的面积依次为
为1,按上述方法所作的正方形的面积依次为 ,
, ,…..,
,….., (n为正整数),那么第8个正方形的面积
(n为正整数),那么第8个正方形的面积 =___________.
=___________.
 ,则AF的长为__________.
,则AF的长为__________.
 是正方形,
是正方形, 垂直于
垂直于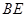 ,且
,且