题目内容
(1)请用两种不同的方法,用尺规在所给的两个矩形中各作一个不为正方形的菱形,且菱形的四个顶点都在矩形的边上.(保留作图痕迹)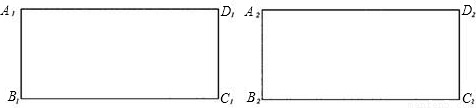
(2)写出你的作法.
【答案】分析:作矩形A1B1C1D1四条边的中点E1,F1,G1,H1;连接H1E1,E1F1,G1F1,G1H1.四边形E1F1G1H1即为菱形;
还可以在B2C2上取一点E2,使E2C2>A2E2且E2不与B2重合;以A2为圆心,A2E2为半径画弧,交A2D2于H2;以E2为圆心,A2E2为半径画弧,交B2C2于F2;连接H2F2,则四边形A2E2F2H2为菱形.
解答:解:(1)所作菱形如图①,②所示.
说明:作法相同的图形视为同一种.例如类似图③,图④的图形视为与图②是同一种.
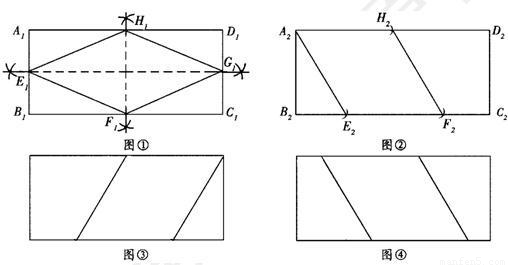
(作出一个图形得3分)
(2)图①的作法:
作矩形A1B1C1D1四条边的中点E1,F1,G1,H1;
连接H1E1,E1F1,G1F1,G1H1.
四边形E1F1G1H1即为菱形.
图②的作法:
在B2C2上取一点E2,使E2C2>A2E2且E2不与B2重合;
以A2为圆心,A2E2为半径画弧,交A2D2于H2;
以E2为圆心,A2E2为半径画弧,交B2C2于F2;
连接H2F2,则四边形A2E2F2H2为菱形.
(写对一个作法得2分)
(此题答案不惟一,只要画法及作法合理,正确,均可酌情得分.)
点评:此题综合考查了菱形和矩形的性质以及一些基本作图的综合应用.
还可以在B2C2上取一点E2,使E2C2>A2E2且E2不与B2重合;以A2为圆心,A2E2为半径画弧,交A2D2于H2;以E2为圆心,A2E2为半径画弧,交B2C2于F2;连接H2F2,则四边形A2E2F2H2为菱形.
解答:解:(1)所作菱形如图①,②所示.
说明:作法相同的图形视为同一种.例如类似图③,图④的图形视为与图②是同一种.

(作出一个图形得3分)
(2)图①的作法:
作矩形A1B1C1D1四条边的中点E1,F1,G1,H1;
连接H1E1,E1F1,G1F1,G1H1.
四边形E1F1G1H1即为菱形.
图②的作法:
在B2C2上取一点E2,使E2C2>A2E2且E2不与B2重合;
以A2为圆心,A2E2为半径画弧,交A2D2于H2;
以E2为圆心,A2E2为半径画弧,交B2C2于F2;
连接H2F2,则四边形A2E2F2H2为菱形.
(写对一个作法得2分)
(此题答案不惟一,只要画法及作法合理,正确,均可酌情得分.)
点评:此题综合考查了菱形和矩形的性质以及一些基本作图的综合应用.

练习册系列答案
相关题目
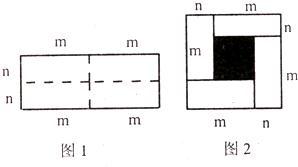
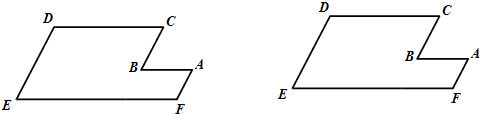
 31、如图是由两个大小不同的正方形与两个全等的长方形拼成的一个大正方形,请用两种不同的方法表示图中空白正方形的面积;
31、如图是由两个大小不同的正方形与两个全等的长方形拼成的一个大正方形,请用两种不同的方法表示图中空白正方形的面积;