题目内容
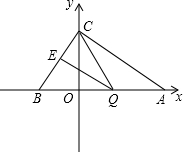
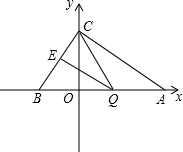 如图,已知在平面直角坐标系中,点A(4,0)、B(-3,0),点C在y轴正半轴上,且tan∠CAO=1,点Q是线段AB上的动点,过点Q作QE∥AC交BC于点E.
如图,已知在平面直角坐标系中,点A(4,0)、B(-3,0),点C在y轴正半轴上,且tan∠CAO=1,点Q是线段AB上的动点,过点Q作QE∥AC交BC于点E.
(1)求点C的坐标及直线BC的解析式;
(2)连结CQ,当△CQE的面积最大时,求点Q的坐标;
(3)若点P是线段AC上的点,是否存在这样的点P,使△PQE成为等腰直角三角形?若存在,试求出所有符合条件的点P的坐标;若不存在,说明理由.
解:(1)∵直角△AOC中tan∠CAO=1,
∴OC=OA=4,
∴C点坐标为(0,4),
设直线BC的解析式是y=mx+n,则 ,
,
解得: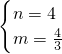
 .
.
则BC所在直线为y= x+4;
x+4;
(2)设直线AC的解析式是y=kx+b,则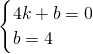 ,
,
解得: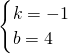 ,
,
则AC所在直线为y=4-x.
设Q点坐标为(q,0),其中q∈[-3,4],则EQ所在直线为y=q-x,
解方程组 ,解得:
,解得: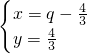 .
.
则E点坐标为( ,
,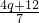 ),
),
S△ABC= AB•OC=
AB•OC= ×7×4=14,
×7×4=14,
AQ=4-q,BQ=q+3,
∵QE∥AC,
∴△BEQ∽△BCA,
∴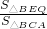 =(
=(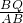 )2=
)2=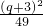 ,
,
∴S△BEQ=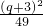 ×14=
×14=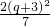 ,
,
S△ACQ= AQ•OC=
AQ•OC= (4-q)×4=2(4-q),
(4-q)×4=2(4-q),
∴S△CEQ=S△ABC-S△BEQ-S△ACQ=14-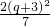 -2(4-q)
-2(4-q)
=-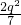 +
+ +
+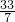 ,
,
则当q= 时,△CEQ的面积最大,则Q的坐标是(
时,△CEQ的面积最大,则Q的坐标是( ,0);
,0);
(3)设P点坐标为(p,4-p) 其中p∈[0,4],
可得PQ2=(p-q)2+(4-p)2
PE2=(p-q+ )2+(4-p-
)2+(4-p- )2
)2
QE2=( )2+(
)2+( )2=
)2= ,
,
△PQE成为等腰直角三角形
(1)PQ为斜边,则有 PE2=QE2
PQ2=2QE2的可得到(p-q+ )2+(4-p-
)2+(4-p- )2=
)2= ,
,
(p-q)2+(4-p)2=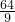 ,
,
解得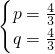 或
或  .
.
其中q= 与q∈[-3,4]的范围不符 所以p=
与q∈[-3,4]的范围不符 所以p= ,q=
,q= ,
,
对应P点坐标为( ,
, )Q点坐标为(
)Q点坐标为( ,0);
,0);
(2)PE为斜边 则有 PQ2=QE2PE2=2QE2即 (p-q)2+(4-p)2=
(p-q+ )2+(4-p-
)2+(4-p- )2=
)2=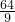
可解得 ,对应P点坐标为(
,对应P点坐标为( ,
, )Q点坐标为(
)Q点坐标为( ,0);
,0);
(3)QE为斜边则有 PQ2=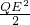 ,PE2=
,PE2=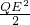
即 (p-q)2+(4-p)2=
(p-q+ )2+(4-p-
)2+(4-p- )2=
)2= ,
,
解得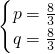 .
.
对应P点坐标为( ,
, )Q点坐标为(
)Q点坐标为( ,0).
,0).
所有符合条件的点P坐标为( ,
, )和(
)和( ,
, ).
).
分析:(1)在直角△AOC中,利用三角函数即可求得OC的长,从而得到C的坐标,利用待定系数法即可求得直线BC的解析式;
(2)设Q的坐标是(q,0),根据相似三角形的性质,用q表示出△BEQ的面积,以及△ACQ的面积,则△CQE的面积即可表示成q的函数,利用函数的性质即可求得q的值;
(3)设P点坐标为(p,4-p),即可利用p、q表示出△PQE的三边的长,然后分三种情况讨论,即可求得p,q的值,从而求得P的坐标.
点评:本题考查了相似三角形的性质,待定系数法求函数的解析式以及二次函数的性质的综合应用,正确进行讨论是关键.
∴OC=OA=4,
∴C点坐标为(0,4),
设直线BC的解析式是y=mx+n,则
 ,
,解得:
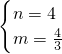
 .
.则BC所在直线为y=
 x+4;
x+4;(2)设直线AC的解析式是y=kx+b,则
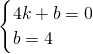 ,
,解得:
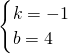 ,
,则AC所在直线为y=4-x.
设Q点坐标为(q,0),其中q∈[-3,4],则EQ所在直线为y=q-x,
解方程组
 ,解得:
,解得: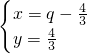 .
.则E点坐标为(
 ,
,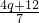 ),
),S△ABC=
 AB•OC=
AB•OC= ×7×4=14,
×7×4=14,AQ=4-q,BQ=q+3,
∵QE∥AC,
∴△BEQ∽△BCA,
∴
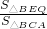 =(
=(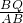 )2=
)2=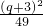 ,
,∴S△BEQ=
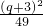 ×14=
×14=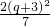 ,
,S△ACQ=
 AQ•OC=
AQ•OC= (4-q)×4=2(4-q),
(4-q)×4=2(4-q),∴S△CEQ=S△ABC-S△BEQ-S△ACQ=14-
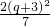 -2(4-q)
-2(4-q)=-
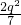 +
+ +
+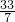 ,
,则当q=
 时,△CEQ的面积最大,则Q的坐标是(
时,△CEQ的面积最大,则Q的坐标是( ,0);
,0);(3)设P点坐标为(p,4-p) 其中p∈[0,4],
可得PQ2=(p-q)2+(4-p)2
PE2=(p-q+
 )2+(4-p-
)2+(4-p- )2
)2QE2=(
 )2+(
)2+( )2=
)2= ,
,△PQE成为等腰直角三角形
(1)PQ为斜边,则有 PE2=QE2
PQ2=2QE2的可得到(p-q+
 )2+(4-p-
)2+(4-p- )2=
)2= ,
,(p-q)2+(4-p)2=
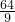 ,
,解得
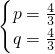 或
或  .
.其中q=
 与q∈[-3,4]的范围不符 所以p=
与q∈[-3,4]的范围不符 所以p= ,q=
,q= ,
,对应P点坐标为(
 ,
, )Q点坐标为(
)Q点坐标为( ,0);
,0);(2)PE为斜边 则有 PQ2=QE2PE2=2QE2即 (p-q)2+(4-p)2=

(p-q+
 )2+(4-p-
)2+(4-p- )2=
)2=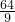
可解得
 ,对应P点坐标为(
,对应P点坐标为( ,
, )Q点坐标为(
)Q点坐标为( ,0);
,0);(3)QE为斜边则有 PQ2=
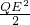 ,PE2=
,PE2=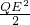
即 (p-q)2+(4-p)2=

(p-q+
 )2+(4-p-
)2+(4-p- )2=
)2= ,
,解得
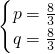 .
.对应P点坐标为(
 ,
, )Q点坐标为(
)Q点坐标为( ,0).
,0).所有符合条件的点P坐标为(
 ,
, )和(
)和( ,
, ).
).分析:(1)在直角△AOC中,利用三角函数即可求得OC的长,从而得到C的坐标,利用待定系数法即可求得直线BC的解析式;
(2)设Q的坐标是(q,0),根据相似三角形的性质,用q表示出△BEQ的面积,以及△ACQ的面积,则△CQE的面积即可表示成q的函数,利用函数的性质即可求得q的值;
(3)设P点坐标为(p,4-p),即可利用p、q表示出△PQE的三边的长,然后分三种情况讨论,即可求得p,q的值,从而求得P的坐标.
点评:本题考查了相似三角形的性质,待定系数法求函数的解析式以及二次函数的性质的综合应用,正确进行讨论是关键.

练习册系列答案
相关题目
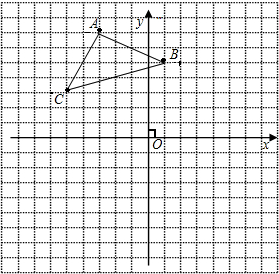 如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),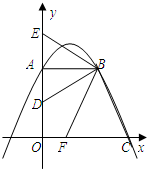 边分别交y轴的正半轴、x轴的正半轴于点E和F.
边分别交y轴的正半轴、x轴的正半轴于点E和F.
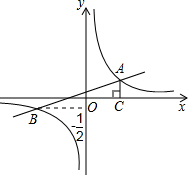 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= 如图,已知在平面直角坐标系中,△ABC的位置如图所示
如图,已知在平面直角坐标系中,△ABC的位置如图所示