Question

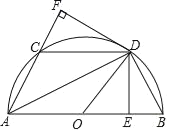
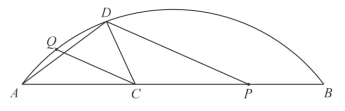
【题目】如图在平面直角坐标系中抛物线经过A（2，0），B（0，4）两点，将△OAB绕点O逆时针旋转90°得到△OCD，点D在抛物线上．

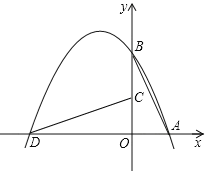
（1）求该抛物线的表达式；

（2）已知点M在y轴上（点M不与点B重合），连接AM，若△AOM与△AOB相似，试求点M的坐标．

Answer 1

【答案】（1）y=-（x-2）（x+4）或y=-x2-x+4；（2）（0，-4）或（0，1）或（0，-1）．

【解析】

(1)根据旋转的性质得到点D的坐标，然后利用待定系数法确定函数解析式；

(2)由于△AOM与△AOB相似且∠AOB=∠AOM=90°．所以应该分两种情况：①若=，即=；②=，即=，通过比例式求得符合条件的m的值即可．

(1)由旋转的性质可得：OD=OB=4，则D(-4，0)．

由抛物线经过点A(2，0)，D(-4，0)．可设y=a(x-2)(x+4)(a≠0)．

把B(0，4)代入，得4=a(0-2)(0+4)．

解得a=-．

故该抛物线解析式为y=-(x-2)(x+4)或y=-x2-x+4．

(2)由题意知，OA=2，OB=4，

设M(0，m)，如图所示，

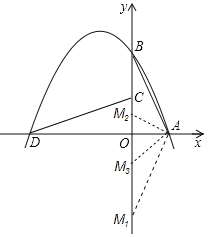
∵△AOM与△AOB相似且∠AOB=∠AOM=90°，

∴分两种情况．

①若=，即=，

解得m=±4，

∵点M不与点B重合，

∴m=-4符合题意，此时M1(0，-4)；

②=，即=，

解得m=±1，

此时M2(0，1)，M2(0，-1)，

综上所述，符合条件的点M的坐标是：(0，-4)或(0，1)或(0，-1)．