题目内容
附加题:如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD。
(1)求证:AB=AD;
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论。
(1)求证:AB=AD;
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论。
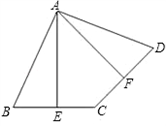
解:(1)证明:连接AC,
∵点E是BC的中点,AE⊥BC,
∴AB=AC,
∵点F是CD的中点,AF⊥CD,
∴AD=AC,
∴AB=AD。
(2)∵∠EAF=∠BAE+∠DAF
证明∵由(1)知AB=AC,即△ABC为等腰三角形
∴AE⊥BC,(已知),
∴∠BAE=∠EAC(等腰三角形的三线合一)
同理,∠CAF=∠DAF
∴∠EAF=∠EAC+∠FAC=∠BAE+∠DAF。

∵点E是BC的中点,AE⊥BC,
∴AB=AC,
∵点F是CD的中点,AF⊥CD,
∴AD=AC,
∴AB=AD。
(2)∵∠EAF=∠BAE+∠DAF
证明∵由(1)知AB=AC,即△ABC为等腰三角形
∴AE⊥BC,(已知),
∴∠BAE=∠EAC(等腰三角形的三线合一)
同理,∠CAF=∠DAF
∴∠EAF=∠EAC+∠FAC=∠BAE+∠DAF。


练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
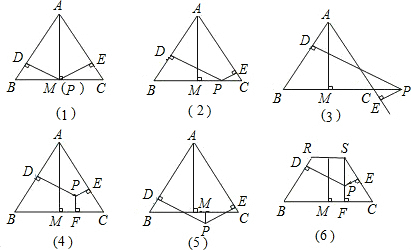
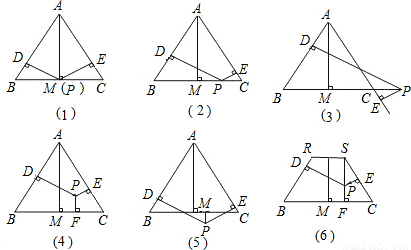
 .图4与图6中的等式有何关系.
.图4与图6中的等式有何关系.
 .图(4)与图(6)中的等式有何关系.
.图(4)与图(6)中的等式有何关系.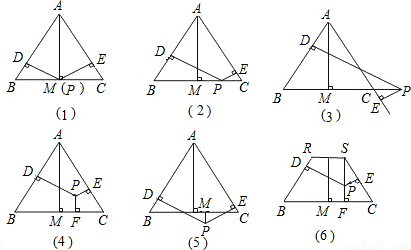
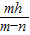 .图(4)与图(6)中的等式有何关系.
.图(4)与图(6)中的等式有何关系.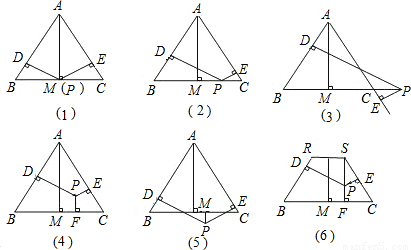
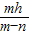 .图(4)与图(6)中的等式有何关系.
.图(4)与图(6)中的等式有何关系.