题目内容
如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的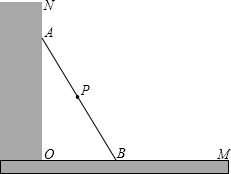 距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
(1)如果木棍的顶端A沿墙下滑0.4米,那么木棍的底端B向外移动多少距离?
(2)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由.
(3)在木棍滑动的过程中,当滑动到什么位置时,△AOB的面积最大?简述理由,并求出面积的最大值.
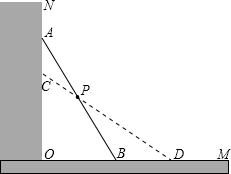 解:(1)在直角△ABC中,已知AB=2.5m,BO=0.7m,
解:(1)在直角△ABC中,已知AB=2.5m,BO=0.7m,则AO=
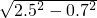 m=2.4m,
m=2.4m,∵AO=AC+OC,
∴OC=2m,
∵直角三角形CDO中,AB=CD,且CD为斜边,
∴OD=
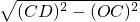 =1.5m,
=1.5m,∴据BD=OD-OB=1.5m-0.7m=0.8m;
(2)不变.
理由:在直角三角形中,斜边上的中线等于斜边的一半,因为斜边AB不变,所以斜边上的中线OP不变;
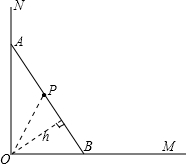
(3)当△AOB的斜边上的高h等于中线OP时面积最大.
如图,若h与OP不相等,则总有h<OP,
故根据三角形面积公式,有h与OP相等时△AOB的面积最大,
此时,S△AOB=
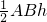 =
= ×2.5×1.25=1.5625.
×2.5×1.25=1.5625.所以△AOB的最大面积为1.5625m2.
分析:(1)在直角三角形ABC中,已知AB,BC根据勾股定理即可求AO的长度,根据AO=AC+OC即可求得OC的长度,在直角三角形CDO中,已知AB=CD,CO即可求得OD的长度,根据BD=OD-OB即可求得BD的长度.
(2)木棍滑动的过程中,点P到点O的距离不会变化.根据在直角三角形中,斜边上的中线等于斜边的一半即可判断;
(3)当△AOB的斜边上的高h等于中线OP时,△AOB的面积最大,就可以求出.
点评:此题考查了勾股定理的应用,利用了在直角三角形中,斜边上的中线等于斜边的一半;同时理解△AOB的面积什么情况最大是解决本题的关键.

练习册系列答案
相关题目
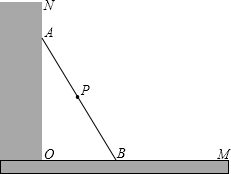 距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行. 棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.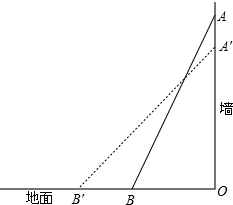 如图所示,一根长25米的梯子,斜立在一竖直的墙上,这时梯子底部距离墙底端7米.如果梯子的顶端沿墙下滑4米后停止,那么梯子的底端将滑动
如图所示,一根长25米的梯子,斜立在一竖直的墙上,这时梯子底部距离墙底端7米.如果梯子的顶端沿墙下滑4米后停止,那么梯子的底端将滑动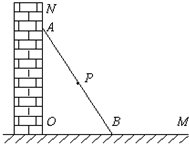 如图所示,一根长2.5m的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时AO的距离为2.4m.若木棍A端沿墙下滑,则B端沿地面向右滑行.
如图所示,一根长2.5m的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时AO的距离为2.4m.若木棍A端沿墙下滑,则B端沿地面向右滑行.