题目内容
如图,AB是半圆O的直径,延长AB至点C,使OB=BC,OC=4,点P是半圆上一动点(不与点A、点B重合),∠ACP=α,则α的取值范围是 .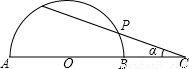
【答案】分析:当点P在半圆上运动时,有α>0,当CP为圆O的切线时,α最大,此时连接OP即为圆的半径,根据切线性质得到OP⊥PC,即三角形OPC为直角三角形,由OB=BC=OP= OC,利用直角三角形中一直角边等于斜边的一半,则这条直角边所对的角为30°,得到α的最大值为30°,写出α的取值范围即可.
OC,利用直角三角形中一直角边等于斜边的一半,则这条直角边所对的角为30°,得到α的最大值为30°,写出α的取值范围即可.
解答: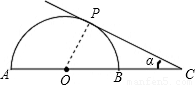 解:当CP与半圆O相切时,如图所示,连接OP,
解:当CP与半圆O相切时,如图所示,连接OP,
由切线的性质得到OP⊥PC,即△OPC为直角三角形,
又OB=BC= OC=2,则圆的半径r=2,即OP=2,
OC=2,则圆的半径r=2,即OP=2,
∴OP= OC,
OC,
则α=30°,
根据题意得到α的范围是:0<α≤30°.
故答案为:0<α≤30°
点评:此题考查学生掌握切线的性质即圆的切线垂直于经过切点的半径,以及直角三角形的性质,考查了数形结合的数学思想,是一道中档题.连接切点与圆心是此类题经常连接的辅助线.
 OC,利用直角三角形中一直角边等于斜边的一半,则这条直角边所对的角为30°,得到α的最大值为30°,写出α的取值范围即可.
OC,利用直角三角形中一直角边等于斜边的一半,则这条直角边所对的角为30°,得到α的最大值为30°,写出α的取值范围即可.解答:
 解:当CP与半圆O相切时,如图所示,连接OP,
解:当CP与半圆O相切时,如图所示,连接OP,由切线的性质得到OP⊥PC,即△OPC为直角三角形,
又OB=BC=
 OC=2,则圆的半径r=2,即OP=2,
OC=2,则圆的半径r=2,即OP=2,∴OP=
 OC,
OC,则α=30°,
根据题意得到α的范围是:0<α≤30°.
故答案为:0<α≤30°
点评:此题考查学生掌握切线的性质即圆的切线垂直于经过切点的半径,以及直角三角形的性质,考查了数形结合的数学思想,是一道中档题.连接切点与圆心是此类题经常连接的辅助线.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm. 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C. 如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是
如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
