题目内容
(2006•贵港)如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4, .
.(1)分别求出A,B两点的坐标;
(2)求此抛物线的函数解析式;
(3)设此抛物线与y轴的交点为C,过
 作直线l与抛物线交于另一点D(点D在x轴上方),连接AC,CB,BD,DA,当四边形ACBD的面积为4时,求点D的坐标和直线l的函数解析式.
作直线l与抛物线交于另一点D(点D在x轴上方),连接AC,CB,BD,DA,当四边形ACBD的面积为4时,求点D的坐标和直线l的函数解析式.
【答案】分析:(1)由已知条件可求出x1,x2的值,A、B的坐标可求.
(2)把A,B的坐标代入二次函数的解析式中,得到关于b,c的方程组,解即可.
(3)此题所给的已知条件有问题.
解答:解:(1)由x1+x2=4,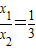 ,
,
得,x1=1,x2=3,(1分)
∴A(1,0),B(3,0).(3分)
(2)把A(1,0),B(3,0)的坐标代入y=-x2+bx+c,
得,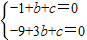 ,(4分)
,(4分)
解得,b=4,c=-3.(5分)
∴所求抛物线的函数解析式为y=-x2+4x-3.(6分)
(3)由题意,设点D的坐标为(f,h),
∵y=-x2+4x-3,
∴点C的坐标为(0,-3),
S△ADB+S△ABC=4,
即 ×2h+
×2h+ ×2×3=4,(7分)
×2×3=4,(7分)
∴h=1,(8分)
∴-f2+4f-3=1,
解得,f1=f2=2,(9分)
∴D(2,1).(10分)
设l的解析式为y=kx+m,
则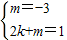 ,
,
∴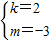 .(11分)
.(11分)
∴l的函数解析式为y=2x-3.(12分)
点评:本题利用了解方程组,以及解一元二次方程等知识.
(2)把A,B的坐标代入二次函数的解析式中,得到关于b,c的方程组,解即可.
(3)此题所给的已知条件有问题.
解答:解:(1)由x1+x2=4,
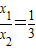 ,
,得,x1=1,x2=3,(1分)
∴A(1,0),B(3,0).(3分)
(2)把A(1,0),B(3,0)的坐标代入y=-x2+bx+c,
得,
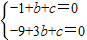 ,(4分)
,(4分)解得,b=4,c=-3.(5分)
∴所求抛物线的函数解析式为y=-x2+4x-3.(6分)
(3)由题意,设点D的坐标为(f,h),
∵y=-x2+4x-3,
∴点C的坐标为(0,-3),
S△ADB+S△ABC=4,
即
 ×2h+
×2h+ ×2×3=4,(7分)
×2×3=4,(7分)∴h=1,(8分)
∴-f2+4f-3=1,
解得,f1=f2=2,(9分)
∴D(2,1).(10分)
设l的解析式为y=kx+m,
则
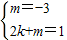 ,
,∴
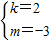 .(11分)
.(11分)∴l的函数解析式为y=2x-3.(12分)
点评:本题利用了解方程组,以及解一元二次方程等知识.

练习册系列答案
相关题目
 x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒
x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒
 x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒
x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒

 .
. 作直线l与抛物线交于另一点D(点D在x轴上方),连接AC,CB,BD,DA,当四边形ACBD的面积为4时,求点D的坐标和直线l的函数解析式.
作直线l与抛物线交于另一点D(点D在x轴上方),连接AC,CB,BD,DA,当四边形ACBD的面积为4时,求点D的坐标和直线l的函数解析式.