题目内容
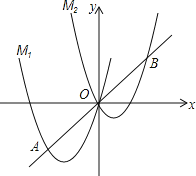
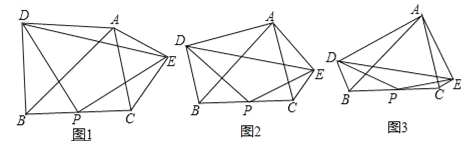
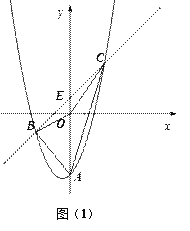
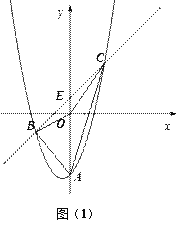
【题目】如图(1),抛物线![]() 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线![]() 与抛物线交于点B、C .
与抛物线交于点B、C .
(1)则点A的坐标是 ______ ;
(2)当b = 0时(如图(2)),△ABE与△ACE的面积大小关系如何?当![]() 时,上述关系还成立吗,为什么?
时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得△BOC是以BC 为斜边的直角三角形,若存在,求出b;若不存在,说明理由.

【答案】(1)(0,-4);(2) 相等,成立,理由见解析;(3)存在, 当b=4或-2时,ΔOBC为直角三角形,理由见解析.
【解析】
解:(1)点A的坐标为(0,-4)
(2)当b=0时,直线为![]()
由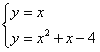
解得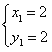 ,
,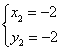
所以B、C的坐标分别为(-2,-2),(2,2)![]() ,
,![]()
所以![]()
当![]() 时,仍有
时,仍有![]() 成立,理由如下
成立,理由如下
由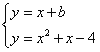
解得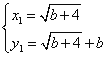 ,
,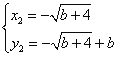
所以B、C的坐标分别为![]() ,
,![]()
![]()
作![]() 轴,
轴,![]() 轴,垂足分别为F、G,则
轴,垂足分别为F、G,则![]()
而![]() 和
和![]() 是同底的两个三角形
是同底的两个三角形
所以![]() (3)存在这样的b
(3)存在这样的b
因为![]()
所以![]()
所以![]() ,即E为BC的中点
,即E为BC的中点
所以当OE=CE时,△OBC为直角三角形
因为![]()
所以![]()
而![]()
所以![]() 解得
解得![]() ,
,![]()
所以当b=4或-2时,ΔOBC为直角三角形

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目