题目内容
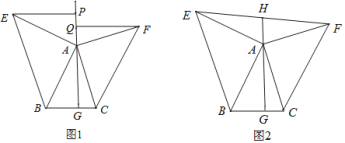
【题目】如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.
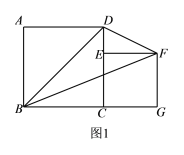
(1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .
(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想;
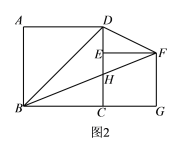
(3)如图2,设BF与CD相交于点H,若△DFH的面积为![]() ,求正方形CEFG的边长.
,求正方形CEFG的边长.
【答案】(1)18,18;(2)S△BDF=![]() S正方形ABCD,证明见解析;(3)4
S正方形ABCD,证明见解析;(3)4
【解析】
(1)根据三角形的面积公式求解;
(2)连接CF,通过证明BD∥CF,可得S△BDF=S△BDC=![]() S正方形ABCD;
S正方形ABCD;
(3)根据S△BDF= S△BDC可得S△BCH= S△DFH=![]() ,由三角形面积公式可求CH,DH的长,再由三角形面积公式求出EF的长即可.
,由三角形面积公式可求CH,DH的长,再由三角形面积公式求出EF的长即可.
(1)∵当点E与点D重合时,
∴CE=CD=6,
∵四边形ABCD,四边形CEFG是正方形,
∴DF=CE=AD=AB=6,
∴S△BDF=![]() ×DF×AB=18,
×DF×AB=18,
当点E为CD的中点时,如图,连接CF,
∵四边形ABCD和四边形CEFG均为正方形;
∴∠CBD=∠GCF=45°,
∴BD∥CF,
∴S△BDF=S△BDC=![]() S正方形ABCD=
S正方形ABCD=![]() ×6×6=18,
×6×6=18,
故答案为:18,18.
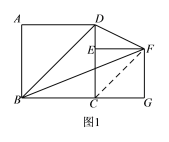
(2)S△BDF=![]() S正方形ABCD,
S正方形ABCD,
证明:连接CF.

∵四边形ABCD和四边形CEFG均为正方形;
∴∠CBD=∠GCF=45°,
∴BD∥CF,
∴S△BDF= S△BDC=![]() S正方形ABCD;
S正方形ABCD;
(3)由(2)知S△BDF= S△BDC,
∴S△BCH= S△DFH=![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴EF=4,
∴正方形CEFG的边长为4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目