题目内容
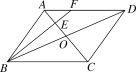
【题目】如图，在ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S△AEF＝4，则下列结论：①
=
；②S△BCE＝36；③S△ABE＝12；④△AEF∽△ACD，其中正确结论是_________.（把正确结论的序号都填上）
【答案】①②③
【解析】
根据平行四边形的性质得到
根据相似三角形的性质得到
等量代换得到
于是得到
；故①正确；根据相似三角形的性质得到S△BCE=36；故②正确；根据三角形的面积公式得到S△ABE=12，故③正确；由于△AEF与△ADC只有一个角相等，于是得到△AEF与△ACD不一定相似，故④错误．
解：∵在ABCD中，
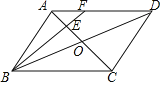
∵点E是OA的中点，
∴
∵AD∥BC，
∴△AFE∽△CBE，
∴
∵AD=BC，
∴
∴ ；故①正确；
∵S△AEF=4， 
∴S△BCE=36；故②正确；
∵
∴
∴S△ABE=12，故③正确；
∵BF不平行于CD，
∴△AEF与△ADC只有一个角相等，
∴△AEF与△ACD不一定相似，故④错误，
故答案为：①②③．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
