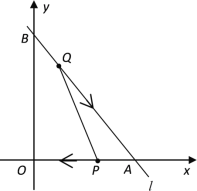
题目内容
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,且
,且![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,动点
两点,动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒2个单位长度的速度向点
上以每秒2个单位长度的速度向点![]() 移动,同时动点
移动,同时动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 移动,设点P、Q移动的时间为
移动,设点P、Q移动的时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() 是以PQ为底的等腰三角形?
是以PQ为底的等腰三角形?
(2)求出点P、Q的坐标;(用含![]() 的式子表达)
的式子表达)
(3)当![]() 为何值时,
为何值时,![]() 的面积是△ABO面积的
的面积是△ABO面积的![]() ?
?
【答案】(1)![]() (2)
(2)![]() 的坐标分别是
的坐标分别是![]() ,(t,0)(3)t1=2秒或,t2=3秒
,(t,0)(3)t1=2秒或,t2=3秒
【解析】
(1)若△APQ是以PQ为底的等腰三角形,那么AQ=AP时,由解析式可得A(6,0),B(0,8),再利用勾股定理得AB=10,然后可以把AQ和AP用t表示,因此得到关于t的方程,解方程即可;
(2)如图,过Q点分别向x轴,y轴引垂线,垂足分别是M,N,设Q(x,y)由题意可知BQ=2t,AP=t,利用△BQN∽△QMA∽△BOA的对应边成比例就可以用t分别表示x、y,也就求出了点P、Q的坐标;
(3)根据(1)(2)知道,△APQ的面积=![]() AP×QM,△AOB的面积=
AP×QM,△AOB的面积=![]() ×6×8=24,因此可以得到关于t的方程,解方程即可解决问题.
×6×8=24,因此可以得到关于t的方程,解方程即可解决问题.
(1)当AQ=AP时,是以PQ为底的等腰三角形.
由解析式可得A(6,0),B(0,8),
由勾股定理得,AB=10,
∴AQ=10-2t,AP=t,
即10-2t=t,
∴![]() (秒)
(秒)
当![]() 时,是以PQ为底的等腰三角形;
时,是以PQ为底的等腰三角形;
(2)过Q点分别向x轴,y轴引垂线,垂足分别是M、N,
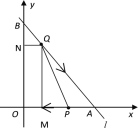
设Q(x,y),由题意可知BQ=2t,AP=t,
△BQN∽△QMA∽△BOA,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() 的坐标分别是
的坐标分别是![]() ,(t,0);
,(t,0);
(3)∵![]() 的面积=
的面积=![]() ,△AOB的面积=
,△AOB的面积=![]() ,
,
∴![]() ,
,
解得t1=2,t2=3,
当t1=2秒或t2=3秒时,![]() 的面积是△ABO面积的
的面积是△ABO面积的![]() .
.

练习册系列答案
相关题目