题目内容
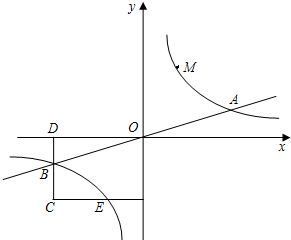 如图,已知双曲线y=
如图,已知双曲线y=| k |
| x |
| 1 |
| 4 |
| k |
| x |
| k |
| x |
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
分析:(1)由BD∥y轴,可知B点与D点的横坐标相等,将x=-8代入直线y=
x,即可求出点B的坐标;再根据A点与B点关于原点对称,求出A点坐标;
(2)先由B是CD中点,D点纵坐标为0,可知B点纵坐标是C点纵坐标的
,即为-
,又B点在直线y=
x上,把y=-
代入直线y=
x,得B点横坐标为-2n,从而可用含n的代数式表示k及E点的坐标,然后根据四边形OBCE的面积=矩形ODCN面积-直角三角形ODB的面积-直角三角形ONE的面积,列出关于n的方程,解方程求出n的值,即可得出C、M两点的坐标,最后运用待定系数法求出直线CM的解析式;
(3)由于点M(m,n)在双曲线y=
上,得出k=mn,再联立双曲线y=
与直线y=
x,求出A、B两点的坐标,由MA=pMP,MB=qMQ求出p、q,从而得出p-q的值.
| 1 |
| 4 |
(2)先由B是CD中点,D点纵坐标为0,可知B点纵坐标是C点纵坐标的
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 4 |
| n |
| 2 |
| 1 |
| 4 |
(3)由于点M(m,n)在双曲线y=
| k |
| x |
| mn |
| x |
| 1 |
| 4 |
解答:解:(1)将x=-8代入直线y=
x,
得y=-2.
∴点B坐标(-8,-2),--(1分)
将点B坐标(-8,-2)代入y=
得:
k=xy=16.--(2分)
∵A点是B点关于原点的对称点,
∴A点坐标为(8,2).--(3分)
(2)∵B是CD中点,C点纵坐标为-n,
∴B点纵坐标为-
,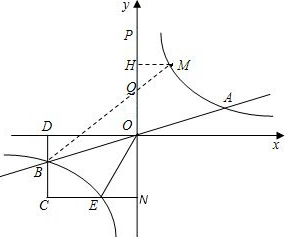
把y=-
代入直线y=
x,得B点横坐标为-2n,
∴D点坐标(-2n,0),B点坐标(-2n,-
),C点坐标(-2n,-n).--(4分)
∴k=(-2n)×(-
)=n2.
将E点纵坐标-n代入方程y=n2/x,得其横坐标-n.
∵四边形OBCE的面积=矩形ODCN面积-Rt△ODB的面积-Rt△ONE的面积,
∴4=2n2-
n2-
n2,
解得n=2.--(5分)
所以C点坐标(-4,-2),M点坐标(2,2)--(6分)
设直线CM的解析式为y=kx+b,则
,
解得
.
∴直线CM解析式为y=
x+
.--(7分)
(3)将点M的坐标(m,n)代入双曲线方程得:k=mn.
双曲线y=
与直线y=
x联立,
解得A点坐标(2
,
),B点坐标(-2
,-
),
∴MA=
,
MP=
,
∵MA=pMP,MB=qMQ,
∴p=
=
,--(9分)
q=
=
,--(11分)
∴p-q=
-
=-2.--(12分)
| 1 |
| 4 |
得y=-2.
∴点B坐标(-8,-2),--(1分)
将点B坐标(-8,-2)代入y=
| k |
| x |
k=xy=16.--(2分)
∵A点是B点关于原点的对称点,
∴A点坐标为(8,2).--(3分)
(2)∵B是CD中点,C点纵坐标为-n,
∴B点纵坐标为-
| n |
| 2 |

把y=-
| n |
| 2 |
| 1 |
| 4 |
∴D点坐标(-2n,0),B点坐标(-2n,-
| n |
| 2 |
∴k=(-2n)×(-
| n |
| 2 |
将E点纵坐标-n代入方程y=n2/x,得其横坐标-n.
∵四边形OBCE的面积=矩形ODCN面积-Rt△ODB的面积-Rt△ONE的面积,
∴4=2n2-
| 1 |
| 2 |
| 1 |
| 2 |
解得n=2.--(5分)
所以C点坐标(-4,-2),M点坐标(2,2)--(6分)
设直线CM的解析式为y=kx+b,则
|

解得
|
∴直线CM解析式为y=
| 2 |
| 3 |
| 2 |
| 3 |
(3)将点M的坐标(m,n)代入双曲线方程得:k=mn.
双曲线y=
| mn |
| x |
| 1 |
| 4 |
解得A点坐标(2
| mn |
| ||
| 2 |
| mn |
| ||
| 2 |
∴MA=
(2
|
MP=
| MH2+HP2 |
∵MA=pMP,MB=qMQ,
∴p=
| MA |
| MP |
2
| ||
| m |
q=
| MB |
| MQ |
2
| ||
| m |
∴p-q=
2
| ||
| m |
2
| ||
| m |
点评:此题综合考查了反比例函数,正比例函数等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 如图,已知双曲线
如图,已知双曲线 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线
如图,已知双曲线