题目内容
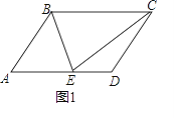
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O,BD=6cm,AD=8cm,AB=10cm,点E从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点G从点C出发,沿CB方向匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动.连接OE,过点G作GF∥BD,设运动时间为t(s)(0<t<4),解答下列问题:
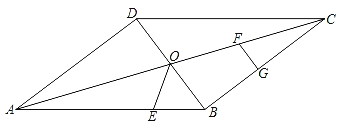
(1)当t为何值时,△BOE是等腰三角形?
(2)设五边形OEBGF面积为S,试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形OEBGF:S△ACD=19:40?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使得OB平分∠COE,若存在,求出t的值;若不存在,请说明理由.
【答案】(1)t为3或![]() 或
或![]() 秒;(2)S五边形BEOFG=﹣
秒;(2)S五边形BEOFG=﹣![]() t+12;(3)2秒;(4)存在t为
t+12;(3)2秒;(4)存在t为![]() 秒时,使OB平分∠COE
秒时,使OB平分∠COE
【解析】
(1)证出△ADB为直角三角形,且∠ADB=90°,分以下三种情况讨论,①当BO=BE时,可得出t=3,②当BO=EO时,如图1,过点O作OH⊥BE于点H,证明△BOH∽△BAD,可得出答案;③当BE=OE,如图2,过点E作EK⊥OB于点K,证明△BEK∽△BAD,由比例线段可得出答案;
(2)证明△CFG∽△COB,求出S△CFG=![]() ,根据S五边形BEOFG=S△BOE+S四边形BOFG可得出答案;
,根据S五边形BEOFG=S△BOE+S四边形BOFG可得出答案;
(3)由(2)的结论可得出t的方程,解方程即可得解;
(4)证明△EOK∽△COB,可得出![]() ,则可得解.
,则可得解.
(1)在△ADB中,
∵AD2+BD2=82+62=100=AB2,
∴△ADB为直角三角形,且∠ADB=90°,
若△BOE为等腰三角形,分以下三种情况讨论,
①当BO=BE时,
t=3,
②当BO=EO时,如图1,过点O作OH⊥BE于点H,
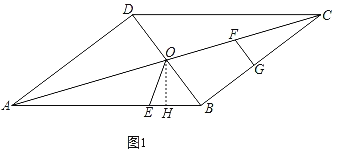
∵∠ABD=∠ABD,∠OHB=∠ADB=90°,
∴△BOH∽△BAD,
∴![]() ,
,
即![]() ,
,
则BH=![]() ,OH=
,OH=![]() ,
,
∵OE=OB,OH⊥BE,
∴BH=![]() BE,
BE,
即![]() ,
,
∴t=![]() ,
,
③当BE=OE,如图2,
过点E作EK⊥OB于点K,
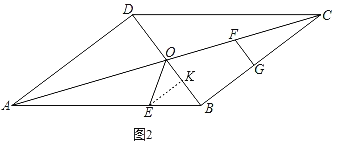
∵∠ABD=∠ABD,∠BKE=∠ADB=90°,
∴△BEK∽△BAD,
∴![]() ,
,
即![]() ,
,
∴BK=![]() t,EK=
t,EK=![]() t,
t,
∵OE=EB,EK⊥BO,
∴BK=![]() BO,
BO,
即![]() ,
,
∴t=![]() ,
,
答:当t为3或![]() 或
或![]() 秒时,△BOE是等腰三角形;
秒时,△BOE是等腰三角形;
(2)∵GF∥BD,
∴∠CFG=∠COB,∠CGF=∠CBO,
∴△CFG∽△COB,
∴![]() ,
,
∴S△CFG=![]() ,
,
∴S四边形BOFG=S△BOC﹣S△CFG=12﹣![]() ,
,
∵S△BOE=![]() BE×OH=
BE×OH=![]() ,
,
∴S五边形BEOFG=S△BOE+S四边形BOFG=12﹣![]() =﹣
=﹣![]() t+12,
t+12,
(3)若S五边形OEBGF:S△ACD=19:40,
∴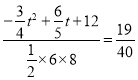 ,
,
整理得:5t2﹣8t﹣4=0,
解得:t1=![]() (舍去),t2=2.
(舍去),t2=2.
答:存在t为2秒时,使S五边形OEBGF:S△ACD=19:40;
(4)若OB平分∠COE,
则∠BOE=∠BOC,∠EKO=∠CBO=90°,
∴△EOK∽△COB,
∴![]() ,
,
∴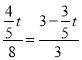 ,
,
解得:t=![]() .
.
答:存在t为![]() 秒时,使OB平分∠COE.
秒时,使OB平分∠COE.

 阅读快车系列答案
阅读快车系列答案【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
![]() 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价;
![]() 若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
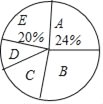
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?