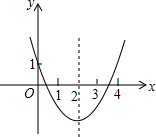题目内容
抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求此抛物线的解析式;
(2)抛物线上是否存在点P,使 ,若存在,求出P点坐标;若不存在,请说明理由.
,若存在,求出P点坐标;若不存在,请说明理由.
(1)求此抛物线的解析式;
(2)抛物线上是否存在点P,使
 ,若存在,求出P点坐标;若不存在,请说明理由.
,若存在,求出P点坐标;若不存在,请说明理由.(1)y=-x2+2x+3;(2) P坐标为(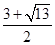 ,
,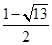 )、(
)、(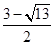 ,
,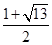 );(
);(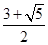 ,
,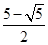 );
);
(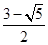 ,
,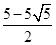 ).
).
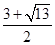 ,
,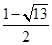 )、(
)、(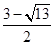 ,
,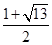 );(
);(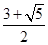 ,
,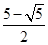 );
);(
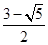 ,
,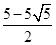 ).
).试题分析:(1)设出抛物线的顶点形式为y=a(x-1)2+4,将A坐标代入求出a的值,即可确定出抛物线解析式;
(2)存在,设出P(a,-a2+2a+3),直线AB解析式为y=kx+b,将A与B坐标代入求出k与b的值,确定出直线AB解析式,根据三角形ABP面积为三角形ABC面积的一半,由两三角形都以AB为底边,得到C到直线AB的距离为P到直线AB距离的2倍,利用点到直线的距离公式列出关于a的方程,求出方程的解得到a的值,即可确定出满足题意P的坐标.
试题解析:(1)设抛物线的顶点形式为y=a(x-1)2+4,
将A(3,0)代入得:0=4a+4,即a=-1,
则抛物线解析式为y=-(x-1)2+4=-x2+2x+3;
(2)存在这样的P点,
设P(a,-a2+2a+3),
设直线AB解析式为y=kx+b,
将A(3,0),B(0,3)代入得:
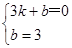 ,
,解得:
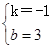 ,
,∴直线AB解析式为y=-x+3,
∵S△ABP=
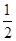 S△ABC,且两三角形都以AB为底边,
S△ABC,且两三角形都以AB为底边,∴P到直线AB的距离等于C到直线AB距离的
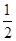 ,
,∵C(1,4)到直线AB的距离d=
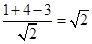 ,
,∴P到直线AB的距离d=
 ,
,即|-a2+3a|=1,
整理得:a2-3a-1=0或a2-3a+1=0,
解得:a=
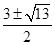 或a=
或a=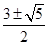
当a=
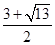 时,-a2+2a+3=-
时,-a2+2a+3=-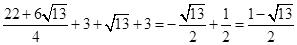 ;
;当a=
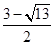 时,-a2+2a+3=-
时,-a2+2a+3=-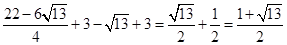 ;
;当a=
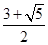 时,-a2+2a+3=-
时,-a2+2a+3=-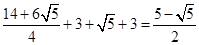 ;
;当a=
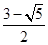 时,-a2+2a+3=-
时,-a2+2a+3=-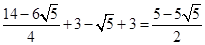 .
.则满足题意的P坐标为(
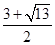 ,
,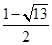 )、(
)、(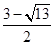 ,
,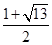 );(
);(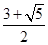 ,
,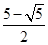 );
);(
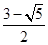 ,
,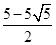 ).
).考点: 1.待定系数法求二次函数解析式;2.二次函数的性质.

练习册系列答案
相关题目
 的图象最高点的纵坐标为0,则m的值为
的图象最高点的纵坐标为0,则m的值为 
 的图像向下平移2个单位后经过点(1,3),那么
的图像向下平移2个单位后经过点(1,3),那么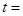 .
.
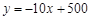 .
.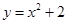 的顶点坐标是( )
的顶点坐标是( )