题目内容
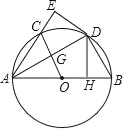
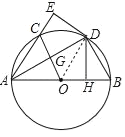
【题目】如图,Rt△ADB中,∠ADB=90°,∠DAB=30°,⊙O为△ADB的外接圆,DH⊥AB于点H,现将△AHD沿AD翻折得到△AED,AE交⊙O于点C,连接OC交AD于点G.
(1)求证:DE是⊙O的切线;
(2)若AB=10,求线段OG的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接半径,由同圆的半径相等得:OA=OD,利用等边对等角可知:∠OAD=∠ODA,利用翻折的性质可知:∠OAD=∠EAD,∠E=∠AHD=90°,证OD∥AE,得∠ODE=90°,所以DE与⊙O相切;
(2)先证明△OAC是等边三角形,再证明OG∥BD,根据中位线定理可知:BD=2OG=5,于是得到结论.
解:(1)连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
由翻折得:∠OAD=∠EAD,∠E=∠AHD=90°,
∴∠ODA=∠EAD,
∴OD∥AE,
∴∠E+∠ODE=180°,
∴∠ODE=90°,
∴DE与⊙O相切;
(2)∵将△AHD沿AD翻折得到△AED,
∴∠OAD=∠EAD=30°,
∴∠OAC=60°,
∵OA=OD,
∴△OAC是等边三角形,
∴∠AOG=60°,
∵∠OAD=30°,
∴∠AGO=90°,
∴OG=![]() AO=
AO=![]() .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目