题目内容
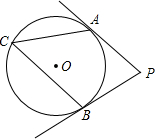 (2013•天津)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为
(2013•天津)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为55
55
(度).分析:首先连接OA,OB,由PA、PB分别切⊙O于点A、B,根据切线的性质可得:OA⊥PA,OB⊥PB,然后由四边形的内角和等于360°,求得∠AOB的度数,又由圆周角定理,即可求得答案.
解答: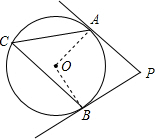 解:连接OA,OB,
解:连接OA,OB,
∵PA、PB分别切⊙O于点A、B,
∴OA⊥PA,OB⊥PB,
即∠PAO=∠PBO=90°,
∴∠AOB=360°-∠PAO-∠P-∠PBO=360°-90°-70°-90°=110°,
∴∠C=
∠AOB=55°.
故答案为:55.
 解:连接OA,OB,
解:连接OA,OB,∵PA、PB分别切⊙O于点A、B,
∴OA⊥PA,OB⊥PB,
即∠PAO=∠PBO=90°,
∴∠AOB=360°-∠PAO-∠P-∠PBO=360°-90°-70°-90°=110°,
∴∠C=
| 1 |
| 2 |
故答案为:55.
点评:此题考查了切线的性质以及圆周角定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 (2013•天津)如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
(2013•天津)如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )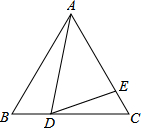 (2013•天津)如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为
(2013•天津)如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为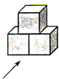 (2013•天津)如图是由3个相同的正方体组成的一个立体图形,它的三视图是( )
(2013•天津)如图是由3个相同的正方体组成的一个立体图形,它的三视图是( ) (2013•天津)如图,是一对变量满足的函数关系的图象,有下列3个不同的问题情境:
(2013•天津)如图,是一对变量满足的函数关系的图象,有下列3个不同的问题情境: