题目内容
（2009•甘孜州）如图，在半径为10的⊙O中，如果弦心距OC=6，那么弦AB的长等于16
16
．分析：先连接OB，由于OC⊥AB可知AB=2BC，在Rt△OBC中利用勾股定理求出BC的长，进而可得出结论．
解答：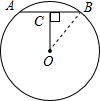
解：连接OB，
∵OC⊥AB，
∴AB=2BC，
在Rt△OBC中，
∵OB=10，OC=6，
∴BC=
=
=8，
∴AB=2BC=2×8=16．
故答案为：16．
解：连接OB，∵OC⊥AB，
∴AB=2BC，
在Rt△OBC中，
∵OB=10，OC=6，
∴BC=
| OB2-OC2 |
| 102-62 |
∴AB=2BC=2×8=16．
故答案为：16．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
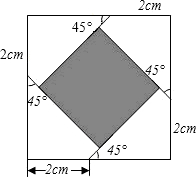（2009•甘孜州）现有若干张边长不相等但都大于6cm的正方形纸片，从中任选一张，如图从距离正方形的四个顶点2cm处，沿45°角画线，将正方形纸片分成5部分，则中间阴影部分的面积是
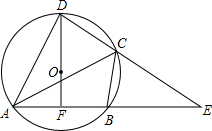（2009•甘孜州）已知：如图，圆内接四边形ABCD的两边AB，DC的延长线相交于点E，DF经过⊙O的圆心，交AB于点F，AB=BE，连接AC，且OD=3，FA=FB=