Question

【题目】如图，点O是等边三角形ABC内一点，∠AOB=110°，∠BOC=β．将△BOC绕点C按顺时针方向旋转60°得到△ADC，连接OD．

（1）求证：△COD是等边三角形；

（2）当β=150°时，试判断△AOD的形状，并说明理由；

（3）探究：当β为多少度时，△AOD是以OD为底边的等腰三角形？

Answer 1

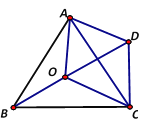
【答案】（1）证明见解析；（2）△AOD是直角三角形，理由见解析；（3）125°．

【解析】

（1）根据图形旋转的性质，得OC=DC，∠OCD=60°，进而即可得到结论；

（2）由等边三角形的性质得∠ODC=60°，结合∠ADC=∠BOC=β=150°，即可得到结论；

（3）由题意得∠AOD=β-60°，结合周角的定义，列出关于β的方程，即可求解．

（1）∵将△BOC绕点C按顺时针方向旋转60°得到△ADC，

∴ OC=DC，∠OCD=60°，

∴△COD是等边三角形；

（2）△AOD是直角三角形，理由如下：

∵△COD是等边三角形，

∴∠ODC=60°，

∵∠ADC=∠BOC=β=150°，

∴∠ADO=∠ADC-∠CDO=150°-60°=90°，

∴△AOD是直角三角形；

（3） ∵△AOD是以OD为底边的等腰三角形，

∴∠ADO=∠AOD=∠ADC-60°=β-60°，

∵110°+β+（60°+∠AOD）=360°，

∴110°+β+（60°+β-60°）=360°，

∴β=125°，

∴当β=125°时，△AOD是以OD为底边的等腰三角形．