题目内容
已知如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，且AD=2cm，AB=3cm，DC=5cm．（1）求下底BC的长为多少？
（2）求该梯形的面积．
【答案】分析：（1）过点D作DE⊥BC于E，在Rt△DCE中利用勾股定理求出EC的长，即可得到BC；
（2）根据梯形面积的公式通过计算即可得到梯形的面积．
解答：
解：（1）如图所示，过点D作DE⊥BC于E，
∴四边形ABED为矩形，
∴AD=BE=2cm，DE=AB=3cm，
在Rt△DCE中，CE=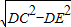
=
=4cm，
∴BC=BE+EC=6cm；
（2）S梯形ABCD=
•（AD+BC）•AB=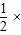
（2+6）×3=12（cm2）．
点评：掌握直角梯形的性质，会求直角梯形的面积问题．
（2）根据梯形面积的公式通过计算即可得到梯形的面积．
解答：
解：（1）如图所示，过点D作DE⊥BC于E，∴四边形ABED为矩形，
∴AD=BE=2cm，DE=AB=3cm，
在Rt△DCE中，CE=
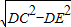==4cm，∴BC=BE+EC=6cm；
（2）S梯形ABCD=
•（AD+BC）•AB=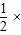（2+6）×3=12（cm2）．点评：掌握直角梯形的性质，会求直角梯形的面积问题．
练习册系列答案
相关题目
