Question

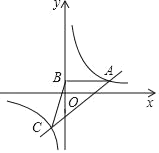
【题目】如图，在平面直角坐标系中，OA=AB，∠OAB=90°，反比例函数y=（x＞0）的图象经过A，B两点．若点A的坐标为（n，1），则 k的值为______．

Answer 1

【答案】

【解析】

作AE⊥x轴于E，BF⊥x轴于F，过B点作BC⊥y轴于C，交AE于G，则 AG⊥BC，先求得△AOE≌△BAG，得出 AG=OE=n，BG=AE=1，从而求得 B（n+1， 1﹣n），根据 k=n×1=（n+1）（1﹣n）得出方程，解方程即可．

作AE⊥x轴于E，BF⊥x轴于F，过B点作BC⊥y轴于C，交AE于G，

如图所示：则AG⊥BC，

∵∠OAB=90°，

∴∠OAE+∠BAG=90°，

∵∠OAE+∠AOE=90°，

∴∠AOE=∠GAB，

在△AOE和△BAG中，，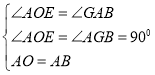

∴△AOE≌△BAG（AAS），

∴OE=AG，AE=BG，

∵点A（n，1），

∴AG=OE=n，BG=AE=1，

∴B（n+1，1﹣n），

∴k=n×1=（n+1）（1﹣n），整理得：n2+n﹣1=0，

解得：n= （负值舍去），

∴n= ，

∴k=；

故答案为：．