题目内容
如图,AB为⊙O的直径,BC为弦,且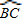 =4
=4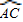 ,则∠AOC= °,∠B= °,∠BOC= °.
,则∠AOC= °,∠B= °,∠BOC= °.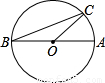
【答案】分析:由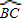 =4
=4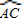 ,得∠BOC=4∠AOC,而∠BOC+∠AOC=180°,则可求出∠AOC,∠BOC,利用圆周角定理可得到∠B的度数.
,得∠BOC=4∠AOC,而∠BOC+∠AOC=180°,则可求出∠AOC,∠BOC,利用圆周角定理可得到∠B的度数.
解答:解:∵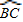 =4
=4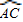 ,
,
∴∠BOC=4∠AOC,
而∠BOC+∠AOC=180°,
∴5∠AOC=180°,
即∠AOC=36°,
∴∠BOC=4×36°=144°,
∴∠B= ∠AOC=18°.
∠AOC=18°.
故答案为:36°,18°,144°.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.
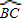 =4
=4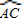 ,得∠BOC=4∠AOC,而∠BOC+∠AOC=180°,则可求出∠AOC,∠BOC,利用圆周角定理可得到∠B的度数.
,得∠BOC=4∠AOC,而∠BOC+∠AOC=180°,则可求出∠AOC,∠BOC,利用圆周角定理可得到∠B的度数.解答:解:∵
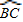 =4
=4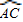 ,
,∴∠BOC=4∠AOC,
而∠BOC+∠AOC=180°,
∴5∠AOC=180°,
即∠AOC=36°,
∴∠BOC=4×36°=144°,
∴∠B=
 ∠AOC=18°.
∠AOC=18°.故答案为:36°,18°,144°.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为