题目内容
13、如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=60°，则∠AED′的度数为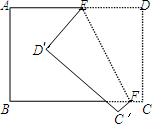
60°
．分析：由四边形ABCD是长方形，根据长方形的性质，即可求得∠DEF的度数，又由折叠的性质，易求得∠DED′的度数，然后由邻补角的定义，即可求得∠AED′的度数．
解答：解：∵四边形ABCD是长方形，
∴AD∥BC，
∴∠DEF=∠EFB=60°，
由折叠的性质可得：∠FED′=∠DEF=60°，
∴∠DED′=120°，
∴∠AED′=180°-∠DED′=60°．
故答案为：60°．
∴AD∥BC，
∴∠DEF=∠EFB=60°，
由折叠的性质可得：∠FED′=∠DEF=60°，
∴∠DED′=120°，
∴∠AED′=180°-∠DED′=60°．
故答案为：60°．
点评：此题考查了长方形的性质与折叠的性质．此题比较简单，解题的关键是注意数形结合思想的应用．
练习册系列答案
教材全解字词句篇系列答案
相关题目
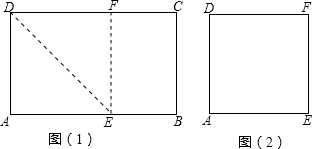
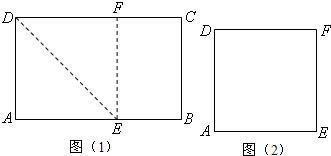24、同学们在小学阶段做过这样的折纸游戏：把一个长方形纸片经过折叠可以得到新的四边形．如图（1），将长方形ABCD沿DE折叠，使点A与点F重合，再沿EF剪开，即得图（2）中的四边形DAEF．
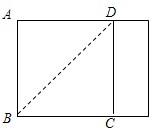27、还记得小时候为了折纸船把长方形的纸截成正方形的方法吗？如图我们把DAB沿着BD对折，使AB于BC重合，然后将右边的矩形撕下，四边形ABCD就是一个正方形了．你能解释这种做法的道理吗？
