题目内容
已知菱形的两条对角线长为8cm和6cm,顺次连接这个菱形的各边中点,所得的是四边形是
矩形
矩形
,所得的这个四边形的面积为12
12
cm2.分析:先根据三角形的中位线平行于第三边,得出EF∥GH,EH∥FG,再根据两组对边分别平行的四边形是平行四边形得到四边形EFGH是平行四边形,再由菱形的对角线互相垂直,证出?EFGH中有一个角等于90°,则这个四边形为矩形;根据三角形的中位线等于第三边的一半,得出矩形的边长分别是菱形对角线的一半,再由矩形的面积公式即可求解.
解答: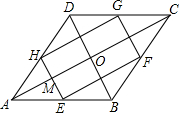 解:如图,菱形ABCD中,对角线AC、BD交于点O,且AC=8cm,BD=6cm,E、F、G、H分别为边AB、BC、CD、DA的中点.
解:如图,菱形ABCD中,对角线AC、BD交于点O,且AC=8cm,BD=6cm,E、F、G、H分别为边AB、BC、CD、DA的中点.
∵E、F、G、H分别为边AB、BC、CD、DA的中点,
∴EF∥AC∥GH,EH∥BD∥FG,
∴四边形EFGH是平行四边形;
∵四边形ABCD是菱形,
∴AC⊥BD,∠AOB=90°,
∵EH∥BD,
∴∠EMO=180°-∠AOB=90°,
∵EF∥AC,
∴∠MEF=180°-∠EMO=90°,
∴?EFGH是矩形;
∵E、F、G、H分别为边AB、BC、CD、DA的中点,
∴EF=GH=
AC=4cm,
EH=FG=
DB=3cm,
∴矩形EFGH的面积为:4×3=12(cm2).
故答案为:矩形,12.
 解:如图,菱形ABCD中,对角线AC、BD交于点O,且AC=8cm,BD=6cm,E、F、G、H分别为边AB、BC、CD、DA的中点.
解:如图,菱形ABCD中,对角线AC、BD交于点O,且AC=8cm,BD=6cm,E、F、G、H分别为边AB、BC、CD、DA的中点.∵E、F、G、H分别为边AB、BC、CD、DA的中点,
∴EF∥AC∥GH,EH∥BD∥FG,
∴四边形EFGH是平行四边形;
∵四边形ABCD是菱形,
∴AC⊥BD,∠AOB=90°,
∵EH∥BD,
∴∠EMO=180°-∠AOB=90°,
∵EF∥AC,
∴∠MEF=180°-∠EMO=90°,
∴?EFGH是矩形;
∵E、F、G、H分别为边AB、BC、CD、DA的中点,
∴EF=GH=
| 1 |
| 2 |
EH=FG=
| 1 |
| 2 |
∴矩形EFGH的面积为:4×3=12(cm2).
故答案为:矩形,12.
点评:本题考查菱形的性质,三角形中位线的性质,矩形的判定及其面积公式,根据三角形中位线的性质得出四边形EFGH的两组对边分别平行及各边的值是解题的关键.

练习册系列答案
相关题目
已知菱形的两条对角线长分别是4cm和8cm,则与此菱形同面积的正方形的边长是( )
| A、8cm | ||
B、4
| ||
C、2
| ||
| D、4cm |
 如图,已知菱形的两条对角线长为a,b,你能将菱形沿对角线分割后拼接成矩形吗?画图说明(拼出一种图形即可);在此过程中,你能发现菱形的面积与a,b的关系吗?
如图,已知菱形的两条对角线长为a,b,你能将菱形沿对角线分割后拼接成矩形吗?画图说明(拼出一种图形即可);在此过程中,你能发现菱形的面积与a,b的关系吗?