题目内容
某商场在销售旺季临近时,某品牌的童装销售价格呈上升趋势,假如这种童装开始时第一周的售价为每件20元,并且从第二周开始每周涨价2元,直到第6周结束,该童装不再销售.(1)请建立一周后每件销售价格y(元)与周次x之间的函数关系式,并写出自变量取值范围.
(2)若该品牌童装于进货当周售完,且这种童装在销售期间每件进价z(元)与周次x之间的关系式为z=-
| 1 | 8 |
分析:(1)根据题意,童装销售价格,第一周的售价为每件20元,并且从第二周开始每周涨价2元,直到第6周结束,分析可得答案;
(2)由(1)的结论,结合题意中的关系式,可得每件获得利润的函数关系式,进而可得答案.
(2)由(1)的结论,结合题意中的关系式,可得每件获得利润的函数关系式,进而可得答案.
解答:解:(1)由题意得,童装销售价格呈上升趋势,
且第一周的售价为每件20元,并且从第二周开始每周涨价2元,直到第6周结束,
当1≤x≤6时,(1分)
y=20+2(x-1)=2x+18(3分)
(2)设每件获得利润为w元,则当1≤x≤6时,
w=y-z(4分)
=2x+18+
(x-8)2-12=
x2+14(6分)
∵
>0,
∴当x>0时,w随x的增大而增大(7分)
∴当x=6时,w最大=18
.(8分)
综上知:在第6周进货并售出后,所获利润最大且为每件18
元(10分).
且第一周的售价为每件20元,并且从第二周开始每周涨价2元,直到第6周结束,
当1≤x≤6时,(1分)
y=20+2(x-1)=2x+18(3分)
(2)设每件获得利润为w元,则当1≤x≤6时,
w=y-z(4分)
=2x+18+
| 1 |
| 8 |
| 1 |
| 8 |
∵
| 1 |
| 8 |
∴当x>0时,w随x的增大而增大(7分)
∴当x=6时,w最大=18
| 1 |
| 2 |
综上知:在第6周进货并售出后,所获利润最大且为每件18
| 1 |
| 2 |
点评:本题考查点二次函数的实际应用,根据题意,建立合适的数学模型,进而由函数的性质可得答案.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
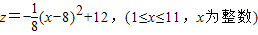 ,那么该品牌童装在第几周售出后,每件获得的利润最大?并求每件的最大利润.
,那么该品牌童装在第几周售出后,每件获得的利润最大?并求每件的最大利润. (x-8)2+12,1≤x≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?
(x-8)2+12,1≤x≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?