题目内容
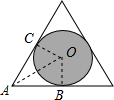
小明随机地在如图所示的正三角形及其内部区域投针，则针扎到其内切圆（阴影）区域的概率为______．
∵如图所示的正三角形，
∴∠CAB=60°，
设三角形的边长是a，
∴AB=
a，
∵⊙O是内切圆，
∴∠OAB=30°，∠OBA=90°，
∴BO=tan30°AB=
a，
则正三角形的面积是
a2，而圆的半径是
a，面积是
a2，
因此概率是
a2÷
a2=
π．
故答案为：
π．
∴∠CAB=60°，
设三角形的边长是a，
∴AB=
| 1 |
| 2 |
∵⊙O是内切圆，
∴∠OAB=30°，∠OBA=90°，
∴BO=tan30°AB=
| ||
| 6 |
则正三角形的面积是
| ||
| 4 |
| ||
| 6 |
| π |
| 12 |
因此概率是
| π |
| 12 |
| ||
| 4 |
| ||
| 9 |
故答案为：
| ||
| 9 |
练习册系列答案
智能训练练测考系列答案
相关题目
