题目内容
【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=![]() ,线段AB的中点表示的数为
,线段AB的中点表示的数为![]() .
.
(问题情境)如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.
(综合运用)(1)点B表示的数是__________.
(2)若BC:AC=4:7,求点C到原点的距离.
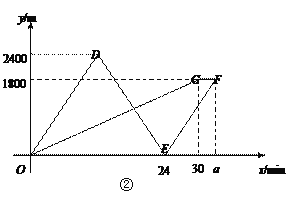
(3)如图2,在(2)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(4)如图3,在(2)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒,1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问PT-MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.

【答案】(1)-20;(2)100;(3)9个单位长度/秒;(4)PT-MN的值不变,值为30.
【解析】
(1)根据AB=60,点A对应的数是40,得出点B对应的数;(2)根据AB=60,BC:AC=4:7,得出BC=80,利用点A对应的数是40,即可得出点C对应的数;(3)假设点R速度为a单位长度/秒,根据点P、Q之间的距离与点Q、R的距离相等,得出等式方程求出即可;(4)分别表示出PT,MN的值,进而求出PT-MN的值;
解:
(1)∵AB=60,点A对应的数是40,
∴点B对应的数为:40-60=-20;
故答案为-20;
(2)∵BC:AC=4:7,
∴BC:AB=4:3,
∵AB=60,
∴BC=80,
∴AC=140,
∵点A对应的数是40,
∴点C对应的数为40-140=-100;
∴C到原点的距离为100;
故答案为100;
(3)设R的速度为a个单位长度/秒,则P的速度为3a个单位长度/秒,Q的速度为(2a-5)个单位长度/秒;
由题意得:![]() ,
,
解得:![]() ,
,
![]() ,
,
答:Q的速度为9个单位长度/秒.
(4)PT-MN的值不变;
理由如下:设运动时间为t 秒,则P:![]() ,
,
T:![]() ,
,
M:![]() ,
,
O:0,
R:![]() ,
,
N:![]() ,
,
PT![]() ,
,
MN![]() ,
,
PT-MN![]() ;
;