题目内容
【题目】下列命题中,其中正确的命题个数有( )
(1)在△ABC中,已知AB=6,AC=2![]() ,∠B=45°,则∠C的度数为60°;
,∠B=45°,则∠C的度数为60°;
(2)已知⊙O的半径为5,圆心O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有3个;
(3)圆心角是180°的扇形是一个半圆;
(4)已知点P是线段AB的黄金分割点,若AB=1,则AP=![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
(1)作出图形,过点A作AD⊥BC于点D,然后求出AD的长度,再在Rt△ACD中,利用锐角的正弦值求出∠C的度数即可;
(2)作出图形,根据圆的半径为5,圆心到AB的距离为3作出到直线AB的距离为2的直线,与圆的交点的个数即为所求;
(3)根据半圆的圆心角等于180°解答;
(4)因为AP是较长的线段还是较短的线段不明确,所以分两种情况讨论求解.
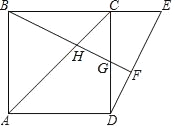
(1)如图,过点A作AD⊥BC于点D,
∵AB=6,∠B=45°,
∴AD=ABsin45°=6×![]() =3
=3![]() ,
,
又∵AC=2![]() ,
,
∴sin∠C=![]() ,
,
∴∠C=60°,故本小题正确;
(2)如图所示,到直线AB的距离为2的点有3个,故本小题正确;
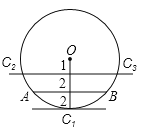
(3)∵半圆的圆心角为180°,
∴圆心角是180°的扇形是一个半圆加一条直径,
故本小题错误;
(4)①若AP是较长线段,则AP2=ABBP,
即AP2=1×(1-AP),
AP2+AP-1=0,
解得AP=![]() ,
,
②若AP是较短的线段,则
AP=1-![]() =
=![]() ,
,
故本小题错误.
综上所述,正确的命题有(1)(2)共2个.
故选B.

 名校课堂系列答案
名校课堂系列答案【题目】九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个选项,每位同学仅选一项,根据调查结果绘制了如下不定整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | 16 |
|
戏剧 | 4 | |
散文 | a |
|
其他 | b | |
合计 | 1 |
根据图表提供的信息,解答下列问题:
(1)直接写出a,b,m的值;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用列表法或画树状图的方法,求选取的2人恰好乙和丙的概率.