Question

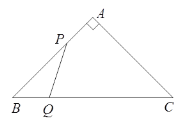
【题目】如图，△ABC是直角边长为1cm的等腰直角三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t（s），解答下列各问题：

（1）当t为何值时，△PBQ是直角三角形？

（2）设四边形APQC的面积为y（cm2），求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是△ABC面积的二分之一？如果存在，求出t的值；不存在，请说明理由．

Answer 1

【答案】（1）t＝－1，2－；（2）不存在t的值，使四边形APQC的面积是△ABC面积的二分之一.

【解析】

（1）分两种情形分别求解即可；

（2）根据S四边形APQC=S△ABC-S△PBQ求解即可；根据四边形APQC的面积是△ABC面积的二分之一，列出方程求解即可；

解：（1）根据题意，BP＝1－t，BQ＝t.

当∠BQP＝90°时，BQ2＋PQ2＝BP2.

因为△ABC是等腰直角三角形，所以∠B＝45°，所以∠BPQ＝45°，所以∠B＝∠BPQ，所以BQ＝QP.

所以2BQ2＝BP2.

所以2t2＝（1－t）2.

解这个方程，得

　 t1＝－1，t2＝－－1＜0，舍去.

当∠BPQ＝90°时，BP2＋PQ2＝BQ2.　

因为△ABC是等腰直角三角形，所以∠B＝45°，所以∠BQP＝45°，所以∠B＝∠B QP，所以BP＝QP.

所以2BP2＝BQ2.所以2（1－t）2＝t2.

解这个方程，得　t1＝2－，t2＝2＋，因为t≤1，所以t2舍去.

综上，t＝－1，2－.

（2）如图，过点P作PH⊥BC于点H.所以BH2＋PH2＝BP2.

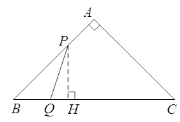
根据题意，BP＝1－t，BQ＝t.

因为△ABC是等腰直角三角形，所以∠B＝45°，所以∠BPH＝45°，所以BH＝PH.

所以2PH2＝BP2，即PH＝BP.

所以PH＝1－t，解得，PH＝（1－t）.

因为S四边形APQC＝S△ABC－S△PBQ.

所以y＝AB×AC－BQ×PH.

　　　y＝×1×1－t×（1－t）

y＝.

不存在t的值，使四边形APQC的面积是△ABC面积的二分之一.

理由如下：

因为S△ABC＝×1×1＝.

所以＝×.

整理，得

　　　　＝0.

△＝－4××1＝2－4＜0，

所以这个一元二次方程无实数解.

所以，不存在t的值，使四边形APQC的面积是△ABC面积的二分之一.